Nick Bostrom

Approved by the examiners:

Professor Elliott Sober and Professor Peter Milne

On July 3^rd, 2000

 

Copyright

 

Email: [email protected]

Personal homepage: http://www.nickbostrom.com

This work is available at: http://www.anthropic-principle.com

---

ABSTRACT

This thesis develops a theory of how to reason when our evidence has been subjected to observational selection effects. It has applications in cosmology, evolutionary biology, thermodynamics and the problem of time’s arrow, game theoretic problems with imperfect recall, the philosophical evaluation of the many-worlds and many-minds interpretations of quantum mechanics and David Lewis’ modal realism, and even for traffic planning.

            After refuting several popular doctrines about the implications of cosmological fine-tuning, we present an informal model of the observational selection effects involved. Next, we evaluate attempts that have been made to codify the correct way of reasoning about such effects – in the form of so-called "anthropic principles" – and find them wanting. A new principle is proposed to replace them, the Self-Sampling Assumption (SSA).

            A series of thought experiments are presented showing that SSA should be used in a wide range of contexts. We also show that SSA gives better methodological guidance than rival principles in a number of scientific fields. We then explain how SSA can lead to the infamous Doomsday argument. Identifying what additional assumptions are required to derive this consequence, we suggest alternative conclusions. We refute several objections against the Doomsday argument and show that SSA does not give rise to paradoxical "observer-relative chances" as has been alleged. However, we discover new consequences of SSA that are more counterintuitive than the Doomsday argument.

            Using these results, we construct a version of SSA that avoids the paradoxes and does not lead to the Doomsday argument but caters to legitimate methodological needs. This modified principle is used as the basis for the first mathematically explicit theory of reasoning under observational selection effects. This observation theory resolves the range of conundrums associated with anthropic reasoning and provides a general framework for evaluating theories about the large-scale structure of the world and the distribution of observers within it.

---

CONTENT

ABSTRACT.......................................................................................................................... 2

CONTENT........................................................................................................................... 3

ACKNOWLEDGEMENTS.................................................................................................. 6

CHAPTER 1: INTRODUCTION.......................................................................................... 8

CHAPTER 2: FINE-TUNING ARGUMENTS IN COSMOLOGY.................................... 15

Does fine-tuning need explaining?................................................................................. 17

Ian Hacking and the Inverse Gambler’s Fallacy............................................................. 20

Robert White and Phil Dowe’s analysis......................................................................... 23

Surprising vs. unsurprising improbable events................................................................ 27

Observational selection effects...................................................................................... 38

Conclusions................................................................................................................. 46

CHAPTER 3: OBSERVATIONAL SELECTION EFFECTS AND THE ANTHROPIC PRINCIPLE            48

The anthropic principle as expressing an observational selection effect........................... 48

Anthropic hodgepodge................................................................................................. 52

Inadequacy of earlier formulations................................................................................. 57

The Self-Sampling Assumption..................................................................................... 61

CHAPTER 4: WHY ACCEPT THE SELF-SAMPLING ASSUMPTION?........................ 64

Prison.......................................................................................................................... 64

Emeralds...................................................................................................................... 67

Two Batches................................................................................................................ 68

God’s Coin Toss.......................................................................................................... 69

The reference class problem......................................................................................... 74

The sampling density.................................................................................................... 78

SSA in cosmology........................................................................................................ 82

SSA in thermodynamics, and time’s arrow.................................................................... 84

SSA in evolutionary biology.......................................................................................... 87

SSA and traffic planning............................................................................................... 92

Summary..................................................................................................................... 93

CHAPTER 5: THE DOOMSDAY ARGUMENT................................................................ 96

Introduction................................................................................................................. 96

Doomsday à la Gott..................................................................................................... 97

The incorrectness of Gott’s argument.......................................................................... 100

Doomsday à la Leslie................................................................................................. 102

The assumptions used in DA, and the Old evidence problem....................................... 105

Leslie on the problem with the reference class............................................................. 114

Alternative conclusions of the Doomsday argument..................................................... 118

CHAPTER 6: SOME ATTEMPTED REFUTATIONS OF THE DOOMSDAY ARGUMENT           120

Objection One........................................................................................................... 120

Objection Two........................................................................................................... 122

Objection Three......................................................................................................... 126

Objection Four.......................................................................................................... 127

Objection Five........................................................................................................... 130

The Self-Indication Assumption.................................................................................. 131

CHAPTER 7: OBSERVER-RELATIVE CHANCES IN ANTHROPIC REASONING?.. 135

Leslie’s argument and why it fails................................................................................ 135

Observer-relative chances: another try........................................................................ 140

Discussion.................................................................................................................. 141

Conclusion................................................................................................................. 146

Appendix................................................................................................................... 146

CHAPTER 8: PARADOXES OF THE SELF-SAMPLING ASSUMPTION.................... 151

Four gedanken wherein SSA yields counterintuitive results.......................................... 151

Discussion of Experiment #2....................................................................................... 154

Discussion of Experiment #4....................................................................................... 162

Conclusion................................................................................................................. 165

Appendix: A SuperNewcomb problem....................................................................... 166

CHAPTER 9: A THEORY OF OBSERVATIONAL SELECTION EFFECTS................. 168

Criteria...................................................................................................................... 169

The outlines of a solution............................................................................................ 170

Formalizing the theory: Equation SSSA-R................................................................... 173

Non-triviality of the reference class............................................................................. 175

SSA and SSSA as special cases of SSSA-R.............................................................. 182

SSSA-R applied to cosmological fine-tuning............................................................... 184

How the observation theory based on SSSA-R measures up against desiderata........... 191

REFERENCES................................................................................................................. 194

---

ACKNOWLEDGEMENTS

I am indebted to more people than I can name. I am grateful to what I think must be literally hundreds of persons, for discussing these issues with me or emailing me thoughtful comments, questions and criticisms. I want to apologize to those who have asked me questions that I have not always had time to give the detailed answers they deserved. Maybe this text will provide a few answers – and hopefully provoke many new questions. Thank you all (you know who you are) for your constant stimulus and feedback!

            There are some people that I want to mention explicitly though. First, I would like to thank my supervisors, Colin Howson and Craig Callender for their continuous trust and support, and for guiding me through the process.

            The following people deserve my sincerest gratitude for their invaluable input in the project: Dennis Dieks, Jacques Mallah, William Eckhardt, Adam Elga, Roger White, Kevin Korb, Jonathan Oliver, Pierre Cruse, Mark Greenberg, Saar Wilf, Wei Dai, Robin Hanson, Paul Franceschi, Hal Finney, Max Tegmark, Jeremy Butterfield, Jean-Michel Delhotel, Richard Swinburne, J-P Delahaye, Bill Jefferys, and to Daniel Hill (who showed how easily breakfasts can extend into lunches when the right quality of philosophical conversation is on the table). I am grateful to my dear friend David Pearce for persuading me to go on-line from the beginning and for helping me in many practical ways. (I will continue to make my working-papers on this subject and other relevant resources available at anthropic-principle.com.) Special thanks are due to Nancy Cartwright, who went out her way to help get me a viva in time to meet a nearly impossible deadline. Thank you, Nancy!

            I am grateful in a superlative way to John Leslie for being helpful and encouraging, for his patience in explaining his views to me when I was new to the field.

            My warm thanks also go to my friend Milan Cirkovic, who steadfastly collaborated with me on an article (on which two paragraphs of chapter 3 are based) from Belgrade while under bombardment during the war between NATO and Serbia.

            I am grateful to several anonymous referees of Mind and Erkenntnis for helpful comments that improved the articles that underlie chapters 6 and 7. I am grateful for audience comments following various presentations of parts of this thesis, particularly from participants at the London School of Advanced Study conference on the Doomsday argument (London, Nov. 6, 1998), which led to improvements of chapter 8. I thank the John Templeton Foundation for a research grant.

            Finally, I would like to thank my friends and family who have supported me. I thank Vassiliki Kambourelli for her unique inspiration and kind assistance during the late stages.

I dedicate this work to my father – med ett varmt, varmt, varmt tack!

 

CHAPTER 1: INTRODUCTION

Anthropic reasoning is a philosophical gold mine. Few philosophical subject matters are as rich in important empirical implications, touch on as many fascinating scientific questions, or contain such generous quantities of conceptual and methodological confusion that needs to be sorted out.

Anthropic principles are used by contemporary cosmologists to derive observational predictions from theories like stochastic inflation which entail the existence of an ensemble of universes. Anthropic coincidences are used by some theists to argue for the existence of a Creator. Others point to anthropic reasoning as providing a counterargument to the cosmological argument for God’s existence. Anthropic constraints have been used to predict how many critical steps there were in the evolution of intelligent life on Earth. The Doomsday argument, using a form of anthropic reasoning, purports to show that the risk that the human species will go extinct fairly soon has been greatly underestimated. One main objection against the many-worlds interpretation of quantum physics draws its force from an implicit appeal to an anthropic principle, as does a common objection against Boltzmann's attempt to explain time’s arrow. There are also applications to game theoretic problems involving imperfect recall and even to traffic planning.

The anthropic principle has to do with observational selection effects. A simple example of a selection effect is if you try to catch fish with a net that doesn’t catch fish shorter than 20 cm. If you use such a net to catch a hundred fish and they all turn out to be 20 cm or longer, then obviously you are not entitled to take this as evidence that the minimum length of fish in the lake is about 20 cm.

            In 1936, The Literary Digest took a phone poll to predict the outcome of the presidential election. Alf Landon was found to be the most popular candidate among those consulted, and so it was predicted that he would win. The prediction, however, failed to take account of an important selection effect owing to the fact that many people did not have telephones at that time. Especially the poor tended to lack telephones and this group also tended to support the rival candidate, Franklin Delano Roosevelt. Roosevelt won a landslide victory. A methodologically more sophisticated approach would either have interviewed a more representative sample set from the population or at least factored in known selection effects.

            Or to take yet another example, suppose you’re a venture capitalist wanting to know what is the average growth rate for companies in the first year after they were founded. You wouldn’t get a very reliable estimate by extrapolating from the data about a hundred companies selected randomly from the Yellow pages in the phone book. It is not uncommon for new companies to fold within a few years, and those who do are much less likely to be listed in the Yellow pages. The companies you find there are typically several years old and can be expected to have performed substantially above average in their first year.

            In these three examples, a selection effect is introduced by the fact that the instrument you use to collect data (a fishing net, a phone poll, the Yellow pages) samples only from a proper subset of the class of entities you are interested in. No different in principle are selection effects introduced not by limitations of some measurement device but by the fact that all observations require the existence of an appropriately positioned observer. The data we have are filtered not only by limitations in our instrumentation but also by the prerequisite that somebody is there to "have" the data yielded by the instruments (and to build the instruments in the first place).

For instance, we find that intelligent life evolved on Earth. It would be a mistake to infer from this that life is likely to evolve on most Earth-like planets. For however small the proportion of all planets that evolved intelligent life, we will find ourselves on a planet that did. (Or we will trace our origin to a planet where intelligent life evolved, in case we are born in a space colony.) The data point – that intelligent life evolved on our planet – is predicted equally by the hypothesis that intelligent life is very improbable even on Earth-like planets and by the hypothesis that intelligent life is probable on Earth-like planets. This data point therefore does not distinguish between the two hypotheses, provided that on both hypotheses intelligent life would have evolved somewhere. (On the other hand, if the "intelligent-life-is-improbable" hypothesis asserted that intelligent life was so improbable that is was unlikely to have evolved anywhere in the whole of cosmos, then the datum that intelligent life evolved on Earth would count against it. For this hypothesis would not have predicted our observation. In fact, it would have predicted that there would have been no observations at all.)

We don’t have to travel for long on the even path of common sense before entering a territory where observational selection effects give rise to difficult and controversial issues. Already in the preceding paragraph we came across a point which is contested. We understood the explanandum – that intelligent life evolved on our planet – in a non-rigid sense. Some authors, however, argue that the explanandum should be, why did intelligent life evolve on this planet (where "this planet" is used as a rigid designator), and that the hypothesis that intelligent life is quite probable on Earth-like planets would indeed give a higher probability to this explanandum (White 1999, Hacking 1987, Dowe 1998). I will show in chapter 2 that this is not the right way to understand the problem.

Notice also that the impermissibility of inferring from the fact that intelligent life evolved on Earth that intelligent life probably evolved on a large fraction of all Earth-like planets does not hinge on the evidence in this example consistings of only one data point. Imagine that we had telepathic abilities and could communicate directly with all other intelligent life that exists in cosmos. Suppose we ask all the aliens, did intelligent life evolve on their planets too? Obviously they would all say: Yes, it did. But equally obvious, this would still not give us any reason to think that intelligent life develops easily. We only asked about the planets where life did in fact evolve (since those planets would be the only ones which would be "theirs" to some alien), and we get no information whatever by hearing the aliens confirming that life evolved on those planets. An observational selection effect vitiates any attempt to gain information by this procedure about how unlikely intelligent life is to evolve. Other considerations would have to be brought to bear if we want to estimate that. (If all the aliens also reported that theirs was some Earth-like planet, this would suggest that intelligent life is unlikely to develop on planets that are not Earth-like – for otherwise some aliens would likely have developed on non-Earth like planets. But it does not tell us whether the evolution of intelligent life on an Earth-like planet is likely or not.)

            One important application and perhaps the earliest one, of anthropic reasoning is to provide a possible (not necessarily the only) explanation of why the universe appears fine-tuned for intelligent life in the sense that if any of various physical constants or initial conditions had been even very slightly different then life as we know it would not have existed. The basic idea behind the possible explanation which uses anthropic reasoning is that the totality of spacetime might be very huge and may contain regions in which the values of fundamental constants and other conditions differ in many ways. (We might also have independent grounds for thinking that that is true.) If this is the case, then we should not be amazed to find that in our own region physical constants and conditions appear "fine-tuned". Owing to an obvious observational selection effect, only such fine-tuned regions are observed. Observing a fine-tuned region is precisely what we should expect if this theory is true, and so it can potentially account for available data in a very neat and simple way, without having to assume that conditions just happened to be "right" through some immensely lucky – and arguably a priori extremely improbable – cosmic coincidence. It also provides an alternative to the hypothesis that our universe was deliberately designed with the intention that it be life-containing.

            Some skeptics doubt the meaningfulness of or need for an explanation of the apparent fine-tuning of our universe. We examine the skeptical arguments in chapter 2 and consider the counterarguments offered by proponents of anthropic explanations of fine-tuning. This leads us into a discussion of the distinction between surprising and unsurprising improbable events, and of what makes a fact cry out for explanation. We find that the anthropic theorizers’ replies fail to meet the skeptics’ challenge. However the intuitions of the former are often correct, and by digging deeper we vindicate those intuitions. This involves constructing an informal model of how observational selection effects operate in the context of cosmological fine-tuning. This model is used to draw a number of additional conclusions about the relative strength of support that various kinds of cosmological theories get from fine-tuning.

While the term "anthropic principle" is less than three decades old, the basic idea of observational selection effects as an important methodological constraint goes back much further. For example, some of the core elements in Kant’s philosophy about how the world of our experience is conditioned on the forms of our sensory and intellectual faculties are not completely unrelated to modern ideas of observational selection effects, although there are fundamental differences. Certainly in Hume’s Dialogues Concerning Natural Religion, one can find early expressions of some ideas of anthropic selection effects. However, it is only quite recently, starting with the works of Brandon Carter (and with some earlier intimations by R. H. Dicke) that the more sophisticated and intricate applications of anthropic reasoning are beginning to be discovered. Many of the most important ideas in this field date back only about a decade or less, philosophers and physicists deserving about equal shares of the credit.

            Chapter 3 discusses some of the many attempts that have been made to codify the modus operandi of anthropic reasoning, often in the form of an "anthropic principle". All of them are to various degrees flawed or inadequate.

In this area confusion reigns supreme. Over twenty anthropic principles have been formulated and many of them have been defined several times over – in nonequivalent ways – by different authors. Some reject anthropic reasoning out of hand as representing an obsolete and irrational form of anthropocentrism. Some hold that anthropic inferences rest on elementary mistakes in probability calculus. Some maintain that at least some of the anthropic principles are tautological and therefore indisputable. Tautological principles have been dismissed by some as empty and thus of no interest or ability to do explanatory work. Others have insisted that like some results in mathematics, though analytically true, anthropic principles can nonetheless be interesting and illuminating. Others still purport to derive empirical predictions from these same principles and regard them as testable hypotheses.

One meta-level reason for thinking that there is something to anthropic reasoning is that it is used and taken seriously by a range of leading physicists and cosmologists. It would be surprising if this bunch of hardheaded scientists were just blowing so much hot air. I hope show that if one peels away extraneous principles, misconceptions, various fallacies and misdescriptions, one can indeed find at the core a set of interesting and useful insights.

It is interesting that so many different and opposing things have been marshaled under the ‘anthropic’ banner. Partly this is due to the philosophical opaqueness of its early formulations and to unfortunate terminological choices. Partly it is due to muddled thinking combined with the well-known capacity of probability theory to generate results that are counterintuitive to some people. But in part it is also due to genuine difficulties intrinsic to this kind of reasoning, some of which are still unresolved. One advantage of having a theory of anthropic reasoning is that we shall be able identify which of its applications uses problematic assumptions and to explicitly state what those assumptions are. But although much useful philosophical analysis of anthropic reasoning has already been done, constructing a theory of observational selection effects cannot be done by merely assembling what is already there. Many of the arguments and principles needed do not yet exist and will have to be invented here as we go along. Also, a number of erroneous doctrines found in the literature need be refuted and corrected.

Chapter 3 ends by proposing what I dub the "Self-Sampling Assumption" as a preliminary formulation (to be revised in chapter 9) of what I take to be the correct basic principle for anthropic reasoning. The content of the Self-Sampling Assumption is unpacked and gradually clarified throughout subsequent chapters.

Chapter 4 gives reasons for accepting the Self-Sampling Assumption. The arguments are of two types. The first type takes the form of thought experiments designed to establish, for a wide range of situations, that it is rational to reason in accordance with the Self-Sampling Assumption. The second type argues that a methodological principle is needed to enable us to derive probabilistic observational consequences from current cosmological theories. I show that while it current rivals fail do this, the Self-Sampling Assumption provides a simple and plausible methodology which coincides with scientific practice and intuitive judgements of what counts as evidence for or against cosmological theories. Support for the Self-Sampling Assumption is also garnered from its useful application in a number of other fields, including evolutionary biology, thermodynamics and even such a mundane activity as traffic planning.

Chapter 5 shows how the Self-Sampling Assumption, when combined with certain other premises, leads to the notorious Doomsday argument. Two different versions of this argument are identified, one of which (the one originated by Richard Gott) is showed to be flawed. The other version, which is due to Brandon Carter and John Leslie, is stronger but nonetheless inconclusive. We identify the critical assumptions that are needed, in addition to the Self-Sampling Assumption, to derive the intended conclusion.

Chapter 6 refutes six recent objections against the Doomsday argument and in the process of doing so throws light on some related issues. Whether the Doomsday argument is sound or not, it shouldn’t be dismissed for the wrong reasons. This is especially important because when the force of the Doomsday argument is appreciated, it gives us valuable clues as to a more satisfactory theory of observational selection effects.

Chapter 7 starts by examining a claim by John Leslie that anthropic reasoning leads to paradoxical observer-relative chances in some types of situations. I show that Leslie’s argument is fallacious. A different type of situation in then described where anthropic reasoning does lead to chances that are observer-relative in an interesting but not paradoxical sense.

While chapters 5-7 to some extent give reassuring messages about the Self-Sampling Assumption as originally formulated, chapter 8 discovers some truly paradoxical apparent consequences of an unrestricted use of that assumption. Among these apparent consequences are that it gives us reason to believe in backward causation, paranormal causation (e.g. psychokinesis) and that it gives advice which seems radically foolish. A careful analysis reveals that the worst of these prima facie consequences are merely apparent. Nonetheless, the fact remains that in some thought experiments the unrestricted use of the Self-Sampling Assumption gives counterintuitive results.

Chapter 9 reexamines the arguments for the Self-Sampling Assumption given in chapter 5 and argues for a modified and relativized version that performs the same useful functions as the original formulation while avoiding the counterintuitive consequences discussed in chapter 8. Taken together with the results from the preceding chapters, this establishes a general framework for modeling reasoning in situations involving conditionalization on information having an indexical component or when our evidence has been subjected to observational selection effects. The relevant probabilistic relation between such evidence and arbitrary hypotheses is given a formal expression in an equation (SSSA-R) and constraints are put in place on a key parameter.

Many valuable specific results and ideas relating to anthropic reasoning have been obtained by various investigators and are used as building blocks here together with many novel ones. This thesis, however, is the first systematic attempt to construct a general and formally explicit theory of reasoning under observational selection effects. It is hoped that it will advance our understanding of the foundational issues in this field and that it will move us closer to being able to tackle those "anthropic problems" – both scientific and philosophical – that still remain mysterious.

CHAPTER 2: FINE-TUNING ARGUMENTS IN COSMOLOGY

The aspect of anthropic reasoning that has received most attention from philosophers is the application in cosmology to explain the apparent fine-tuning of our universe. "Fine-tuning" refers to the supposed fact that there is a set of cosmological parameters or fundamental physical constants which are such that had they been very slightly different then the universe would have been void of intelligent life. For example, in the classical big bang model, the early expansion speed seems fine-tuned. Had it been very slightly greater, the universe would have expanded too rapidly and no galaxies would have formed; there would only have been a very low density hydrogen gas getting more and more dispersed over time. In such a universe, presumably, life could not evolve. Had the early expansion speed been very slightly less, then the universe would have recollapsed within a fraction of a second, and again there would have been no life. Our universe, having just the right conditions for life, appears to be balancing on a knife’s edge (Leslie 1989). A number of other parameters seem fine-tuned in the same sense – e.g. the ratio of the electron mass to the proton mass, the magnitudes of force strengths, the smoothness of the early universe, the neutron-proton mass difference, even the metric signature of spacetime (Tegmark 1997).

            Some philosophers and physicists take fine-tuning to be an explanandum that cries out for an explanans. Two possible explanations are usually envisioned: the design hypothesis and the ensemble hypothesis. Although these explanations are compatible, they tend to be viewed as competing: if we knew that one of them were correct, there would be less temptation to think that the other obtained.

The design hypothesis is that our universe is the result of purposeful design. The "agent" doing the designing need not be a theistic "God", although of course that is one of the archetypal version of the design hypothesis. Other universe-designers have been considered in this context. For example, John Leslie (Leslie 1972, Leslie 1979, Leslie 1989) discusses the case for a neoplatonist "causally efficacious ethical principle", which he thinks might have been responsible for creating the world and giving physical constants and cosmological parameters the numerical values they have. Derek Parfit (Parfit 1998) considers various "universe selection principles", which although they are very different from what people have traditionally thought of as "God" or a "Designer" can nevertheless suitably be grouped under the heading of design hypotheses for present purposes. We can take "purposeful designer" in a very broad sense to refer to any being, principle or mechanism external to our universe responsible for selecting its properties, or responsible for making it in some sense probable that our universe should be fine-tuned for intelligent life. Needless to say, it is possible to doubt the meaningfulness of many of these design hypotheses. Even if one agrees that a given design hypothesis represents a coherent possibility, one may still think that it should be assigned an extremely low degree of credence. For people who are already convinced that there is a God, however, the design hypothesis is apt to be an attractive explanation of why our universe is fine-tuned. And if one is not already convinced about the existence of a Designer, but thinks that it is a coherent possibility, one may be tempted to regard fine-tuning as reason for increasing one’s credence in that hypothesis. One prominent champion of the fine-tuning argument for God’s existence is Richard Swinburne (Swinburne 1991). Several other theologians and philosophers also support this position (see e.g. Craig 1997, Craig 1988, Ross 1992, Polkinghorne 1986, Manson 1989).

The main rival explanation of fine-tuning is the ensemble hypothesis, which states that the universe we observe is only a small part of the totality of physical existence. This totality itself needs not be fine-tuned; if it is sufficiently big and variegated, so that it was likely to contain as a proper part the sort of fine-tuned universe we observe, then an observational selection effect can be invoked to explain why we see a fine-tuned universe. The usual form of the ensemble hypothesis is that our universe is but one in a vast ensemble of actually existing universes, the totality of which we can call "the multiverse", adopting recent terminology. What counts as a universe in such a multiverse is a somewhat vague matter, but "a large, causally fairly disconnected spacetime region" is sufficiently precise for our aims. If the world consists of a sufficiently huge number of such universes, and the values of physical constants vary between these universes according to some suitably broad probability distribution, then it may well be the case that it was quite probable that a fine-tuned universe like ours would come into existence. The actual existence of such a multiverse – an ensemble of "possible universes" would not do – provides the basis on which the observational selection effect operates. The argument then goes like this: Even though the vast majority of the universes are not suitable for intelligent life, it is no wonder that we should observe one of the exceptional universes which are fine-tuned; for the other universes contain no observers and hence are not observed. To observers in such a multiverse, the world will look as if it were fine-tuned. But that is because they see only a small and unrepresentative part of the whole. Observers may marvel at the fact that the universe they find themselves in is so exquisitely balanced, but once they see the bigger picture they can realize that there is really nothing to be astonished by. On the ensemble theory, there had to be such a universe (or at least, it was not so improbable that there would be), and since the other universes have no observers in them, a fine-tuned universe is precisely what the observers should expect to observe given the existence of the ensemble. The multiverse itself need not be fine-tuned. It can be robust in the sense that a small change in its basic parameters would not change the fact that it contains regions where intelligent life exists.

In contrast to some versions of the design hypothesis, the meaningfulness of the ensemble hypothesis is not much in question. Only those subscribing to a very strict verificationist theory of meaning would deny that it is possible that the world might contain a large set of causally fairly disconnected spacetime regions with varying physical parameters. (And even the most hardcore verificationist would be willing to consider at least those ensemble theories according to which other universes are in principle physically accessible from our own universe. Such ensemble theories have been proposed, although they represent only a special case of the general idea.) But there are other philosophical perplexities that arise in this context. One can wonder, for example, in what sense the suggested anthropic explanation of fine-tuning (it is "anthropic" because it involves the idea of an observational selection effect) is really explanatory and how it would relate to a more directly causal account of how our universe came to be. Another important issue is whether fine-tuning provides some evidence for a multiverse. The first question we shall consider, however, is whether fine-tuning stands in any need of explanation at all.

Does fine-tuning need explaining?

First a few words about the supposition that our universe is in fact fine-tuned. This is an empirical assumption which is not entirely trivial. It is certainly true that our current best physical theories, in particular the Grand Unified Theory of the strong, weak, and electromagnetic forces and the big bang theory in cosmology have a number (twenty or so) of free parameters. There is quite strong reason to think at least some of these parameters are fine-tuned – the universe would have been inhospitable to life if their values had been slightly different. (A good overview of the case for fine-tuning is chapter 2 of John Leslie’s (Leslie 1989).) While it is true that our knowledge of exotic life forms possible under a different physics than the actual one is very limited (Wilson 1991, Smith 1985, Feinberg and Shapiro 1980), it does seem quite reasonable to think, for instance, that life would not have evolved if the universe had contained only a highly diluted hydrogen gas or if it had recollapsed within a fraction of a second after big bang (referring to the seeming fine-tuning in the early expansion speed) (Leslie 1985). What little direct evidence we have supports this suggestion. Life does not seem to evolve easily even in a universe like our own, which presumably has rather favorable conditions – complex chemistry, relatively stable environments, large entropy gradients etc. (Hanson 1998, Simpson 1964, Carter 1983, Mayr 1985, Raup 1985, Hart 1982, Papagiannis 1978). There are as yet no signs that life has evolved in the observable universe anywhere outside our own planet (Tipler 1982, Brin 1983).

One should not jump from this to the conclusion that our universe is fine-tuned. For it is possible that some future physical theory will be developed that uses fewer free parameters or uses only parameters on which life does not sensitively depend. However, since the empirical case for fine-tuning is separate from the philosophical problem of how to react if our universe really is fine-tuned, we can set these scruples to one side.[1] Let’s assume the most favorable case for fine-tuning enthusiasts: that the physics of our universe has several independent free parameters which are fine-tuned to an extremely high degree. If that is so, is it something that cries out for explanation or should we be happy to accept it as one of those brute facts that just happen to obtain?

            I suggest that there are two parts to the answer to this question, one of which is fairly unproblematic. This easier part of the answer is as follows: In general, simplicity is one desideratum on plausible scientific theories. Other things equal, we prefer theories which make a small number of simple assumptions to ones that involve a large number of ad hoc stipulations. I see no reason not to apply this methodological principle in cosmology. It is used successfully in the rest of science and indeed has a strong track record within cosmology too.[2] Thus, I think one can admit that there is something dissatisfactory about a cosmological theory which tells us that the universe contains a large number of fine-tuned constants. Such a theory might be true, but we should not be keen to believe that until we have convinced ourselves that there is no simpler theory that can account for the data we have. So if the universe looks fine-tuned, this can be an indication that we should look harder to see if we cannot find a theory which reduces the number of independent assumptions needed. This is one reason for why a universe which looks fine-tuned (whether or not it actually is fine-tuned) is crying out for explanation.

            We should note two things about this easy part of the answer. First, there might not be an explanation even if the universe is "crying out" for one in this sense. There is no guarantee that there is a simpler theory using fewer free parameters which can account for the data. At most, there is a prima facie case for looking for one, and for preferring the simpler theory if one can be found.

Second, the connection to fine-tuning is merely incidental. In this part of the answer, it is not fine-tuning per se, only fine-tuning to the extent that it is coupled to having a wide range of free parameters, that is instigating the search for a better explanation. Fine-tuning is neither necessary nor sufficient for this. It is not sufficient, because in order for a theory to be fine-tuned for intelligent life, it needs to have but a single free parameter. If a theory has a single physical constant on which the existence of intelligent life very sensitively depends, then the theory is fine-tuned. Yet a theory with only one free parameter could be eminently simple. If a universe cries out for explanation even though such a theory accounts for all available evidence, it must clearly be on some other basis than that of a general preference for simpler theories. Also, fine-tuning is not necessary for there to be a cry for explanation. One can imagine a cosmological theory which contains a large number of free parameters but is not fine-tuned because life does not sensitively depend on the values assigned to these parameters.

The easy part of the answer is therefore: Yes, fine-tuning cries out for explanation to the extent to which it is correlated with an excess of free parameters and a resultant lack of simplicity.[3] This part of the answer has been overlooked in discussions of fine-tuning, yet it is important to separate out this aspect in order to rightly grasp the more problematic part to which we shall now turn. The problematic part is to address the question of whether fine-tuning especially cries out for explanation, beyond the general appeal to avoid unnecessary complications and ad hoc assumptions. In other words, is the fact that the universe would have been lifeless if the values of fundamental constants had been very slightly different (assuming this is a fact) relevant in assessing whether an explanation is called for of why the constants have the values they have? And does it give support to the multiverse hypothesis? Or alternatively to the design hypothesis? The rest of this chapter will focus on these questions (though the design hypothesis will be discussed only as it touches on the other two questions).

Ian Hacking and the Inverse Gambler’s Fallacy

Can an anthropic argument based on an observational selection effect together with the assumption that an ensemble of universes exists explain the apparent fine-tuning of our universe? Ian Hacking has argued that this depends on the nature of the ensemble. If the ensemble consists of all possible big-bang universes (a position he ascribes to Brandon Carter) then, says Hacking, the anthropic explanation works:

 

Why do we exist? Because we are a possible universe [sic], and all possible ones exist. Why are we in an orderly universe? Because the only universes that we could observe are orderly ones that support our form of life. …nothing is left to chance. Everything in this reasoning is deductive. (Hacking 1987, p. 337)

 

Hacking contrasts this with a seemingly analogous explanation which seeks to explain fine-tuning by supposing that a Wheeler-type multiverse exists. In the Wheeler cosmology, there is a never-ending sequence of universes each of which begins with a big bang and ends with a big crunch which bounces back in a new big bang, and so forth. The values of physical constants are reset in a random fashion in each bounce, so that we have a vast ensemble of universes with varying properties. The purported anthropic explanation of fine-tuning based on such a Wheeler ensemble notes that given that the ensemble is large enough then it could be expected to contain at least one fine-tuned universe like ours. An observational selection effect can be invoked to explain why we observe a fine-tuned universe rather than one of the non-tuned ones. On the face of it, this line of reasoning looks very similar to the anthropic reasoning based on the Carter multiverse, of which Hacking approves. But according to Hacking, there is a crucial difference. He thinks that the version using the Wheeler multiverse commits what he dubs the "Inverse Gambler’s Fallacy". This is the fallacy of a dim-witted gambler who thinks that the apparently improbable outcome he currently observes is made more probable if there have been many trials preceding the present one.

 

[A gambler] enters the room as a roll is about to be made. The kibitzer asks, ‘Is this the first role of the dice, do you think, or have we made many a one earlier tonight?… slyly, he says ‘Can I wait until I see how this roll comes out, before I lay my bet with you on the number of past plays made tonight?’ The kibitzer… agrees. The roll is a double six. The gambler foolishly says, ‘Ha, that makes a difference – I think there have been quite a few rolls.’ (Hacking 1987, p. 333)

 

The gambler in this example is clearly making a mistake. But it is almost equally clear that Hacking is making a mistake in thinking that the situation is analogous to the one regarding fine-tuning. As was pointed out by three independent authors (Whitaker 1988, McGrath 1988, Leslie 1988) replying to Hacking’s paper, there is no observational selection effect in his example – an essential ingredient in the purported anthropic explanation of fine-tuning.

            One way of introducing an observational selection effect in Hacking’s example is by supposing that the gambler has to wait outside the room until a double six is rolled. Knowing that this is the setup, the gambler does obtain some reason upon entering the room and seeing the double six for thinking that there have probably been quite a few rolls already. This is a closer analogy to the fine-tuning case. The gambler can only observe certain outcomes – we can think of these as the "fine-tuned" ones – and upon observing a fine-tuned outcome he obtains reason to think that there have been several trials. Observing a double six would be surprising on the hypothesis that there were only one roll, but it would be expected on the hypothesis that there were very many. Moreover, a kind of explanation of why the gambler is seeing a double six is provided by pointing out that there were many rolls and the gambler would be let in to observe the outcome only upon rolling a double six. When we make the example more similar to the fine-tuning situation, we find that it supports, rather than refutes, the analogous reasoning based on the Wheeler cosmology.

            What makes Hacking’s position especially peculiar is that he thinks that the anthropic reasoning works with a Carter multiverse but not in a Wheeler universe. Every author I am aware of who has written about this thinks that Hacking is wrong on this point. Many think the anthropic reasoning works in both cases, some think it doesn’t work in either case, but Hacking is probably alone in thinking it works in one but not the other. The only pertinent difference between the two cases seems to be that in the Carter case one deduces the existence of a universe like ours, whereas in the Wheeler case one infers it probabilistically. The Wheeler case can be made to approximate the Carter case by having the probability that a universe like ours should be generated in some cycle be close to 1. (This is in fact the case in the Wheeler scenario if there are infinitely many cycles and there is a fixed finite probability in each cycle of a universe like ours resulting). It is hard to see the appeal of a doctrine that drives a methodological wedge between the two cases, asserting that the anthropic explanation works perfectly in one and works not at all in the other.

Robert White and Phil Dowe’s analysis

A more challenging criticism of the anthropic explanation of fine-tuning has been suggested by Robert White (White 1999) and Phil Dowe (Dowe 1998). They eschew Hacking’s doctrine that there is an essential difference between the Wheeler and the Carter multiverse as regards the correctness of corresponding anthropic fine-tuning explanation. But they take up another idea of Hacking’s, namely that what goes wrong in the Inverse Gambler’s Fallacy is that the gambler fails to regard the most specific version he knows of the explanandum when making his inference to the best explanation. If all the gambler had known were that a double six had been rolled, then it need not have been a fallacy to infer that there probably were quite a few rolls (since that would have made it more probable that there would be at least one double six). However, the gambler knows that this roll – the latest one – was a double six, and this gives him no reason to believe there were many rolls (since the probability that that roll would be a double six is one in thirty-six independently of how many times the dice have been rolled). And, argues Hacking, we have to use the most specific explanandum that we have knowledge of:

 

If F is known, and E is the best explanation of F, then we are supposed to infer E. However, we cannot give this rule carte blanche. If F is known, then FvG is known, but E* might be the best explanation of FvG, and yet knowledge of F gives not the slightest reason to believe E*. (John, an excellent swimmer, drowns in Lake Ontario. Therefore he drowns in either Lake Ontario or the Gulf of Mexico. At the time of his death, a hurricane is ravaging the Gulf. So the best explanation of why he drowned is that he was overtaken by a hurricane, which is absurd.) We must insist that F, the fact to be explained, is the most specific version of what is known and not a disjunctive consequence of what is known. (Hacking 1987, p. 335)

 

Applying this to fine-tuning, Hacking, White and Dowe charge that the purported anthropic explanation of fine-tuning fails to explain the most specific version of what is known. We know not only that some universe is fine-tuned; we know that this universe is fine-tuned. Now, if our explanandum is, Why is this universe fine-tuned? – where "this universe" is understood rigidly–, it would seem that postulating many universes would not go anywhere towards explaining this; nor would it make the explanandum more probable. For how could the existence of many other universes make it more likely that this universe would be fine-tuned?

It is useful at this stage to introduce some abbreviations. In order to focus on the point that White and Dowe are making, we can make some simplifying assumptions.[4] Let us suppose that there are n possible configurations of a big bang universe {T₁, T₂, …, T_n} and that they are equally "probable", P(T_i) = 1/n. We assume that T₁ is the only configuration that permits life to evolve. Let the variable "x" range over the set of actual universes. We assume that each universe instantiates a unique T_i, so that . Let  be the number of actually existing universes, and let "" rigidly denote our universe. We define

 

E := T₁                     (" is life-permitting.")

E’ :=               ("Some universe is life-permitting.")

M := m>>0                  ("There are many universes." – the multiverse hypothesis)

 

White claims that while there being many universes increases the probability that there is a life-permitting universe, P(E’|M) > P(E’|¬M), it is not the case that there being many universes increases the probability that our universe is life-permitting. That is, P(E|M) = P(E|¬M) = 1/n. The argument White gives for this is that

 

the probability of [E, i.e. the claim that  instantiates T₁] is just 1/n, regardless of how many other universes there are, since ’s initial conditions and constants are selected randomly from a set of n equally probable alternatives, a selection which is independent of the existence of other universes. The events which give rise to universes are not causally related in such a way that the outcome of one renders the outcome of another more or less probable. They are like independent rolls of a die. (White 1999, p. 4)

 

Since we should conditionalize on the most specific information we have when evaluating the support for the multiverse hypothesis, and since E’ is more specific than E, White concludes that the our knowledge that our universe permits life to evolve gives us no reason to think there are many universes.

            This argument has some initial plausibility. Nonetheless, I think it is fallacious. We get a hint that something has gone wrong if we pay attention to a certain symmetry of the situation. Let , , …,  be the actually existing universes, and for i =, , …, , let E_i be the proposition that if some universe is life-permitting then i is life-permitting. Thus, E is equivalent to the conjunction of E’ and . According to White, P(M|E’) > P(M) and P(M|E’) = P(M|E) = P(M), which implies P(M|E’) < P(M|E’). Because of the symmetry of the :s, P(M|E’) = c, for every . This entails that P(M|E’) < P(M|E’) for every . In other words, White is committed to the view that, given that some universe is life-permitting, then conditionalizing on  being life-permitting decreases the probability of M, while conditionalizing on any of , …,  increases the probability of M. But this seems wrong. Given that some universe is life-permitting, why should the fact it is this universe that is life-permitting, rather than any of the others, lower the probability that there are many universes? If it had been some other universe instead of this one that had been life-permitting, why should that have made the multiverse hypothesis any more likely? Clearly, such discrimination could be justified only if there were something special that we knew about this universe that would make the fact that it is this universe rather than some other that is life-permitting significant. I can’t see what sort of knowledge that would be. It is true that we are in this universe and not in any other – but that fact presupposes that it is life-permitting. It is not as if there is a remarkable coincidence between our universe being life-permitting and us being in it. So it’s hard to see how the fact that we are in this universe could justify treating its being life-permitting as giving a lower probability to the multiverse hypothesis than any other universe’s being life-permitting would have.

            So what, precisely, is wrong in White’s argument? His basic intuition for why P(M|E) = P(M) seems to be that "The events which give rise to universes are not causally related in such a way that the outcome of one renders the outcome of another more or less probable.". But a little reflection reveals that this statement it is highly problematic for several reasons.

            First, there is no current warrant for making the assertion. Very little is still known about the events which give rise to universes. There are models on which the outcomes of some such events causally influence the outcome of others. To illustrate, in Lee Smolin’s (admittedly highly speculative) evolutionary cosmological model (Smolin 1997), universes create "baby-universes" whenever a black hole is formed, and these baby-universes inherit some of the properties of their parents. The outcomes of chance events in one such conception can thus influence the outcomes of chance events in the births of other universes. Variations of the Wheeler oscillating universe model have also been suggested where some properties are inherited from one cycle to the next. Andrei Linde has speculated about the possibility that advanced civilizations may have the ability to create "basement-universes" and transfer some information into them.

            Even if the events which give rise to universes are not causally related in the sense that the outcome of one event causally influences the outcome of another (as in the above examples), that does not mean that one universe may not carry information about another. For instance, two universes can have a partial cause in common. This is the case in the multiverse models associated with inflation theory (arguably the best current candidates for a multiverse cosmology). In a nutshell, the idea is that universes arise from inflating fluctuations in some background space. The existence of this background space and the parameters of the chance mechanism which lead to the creation of inflating bubbles are at least partial causes of the universes that are produced. The properties of the produced universes could thus carry information about this background space and the mechanism of bubble creation, and hence indirectly also about other universes that have been produced by the same mechanism. The majority of multiverse models that have actually been proposed, including arguably the most plausible one, thus negate White’s categorical statement.

            Second, we can consider the hypothetical case of a multiverse model where the universes bear no causal relations to one another. But even there, it is not clear that that P(M|E) = P(M). We need to make a distinction between objective chance and epistemic probability. If there is no causal connection (whether direct or indirect) between the universes, then there is no correlation in the physical chances of the outcomes of the events in which these universes are created. It doesn’t follow that the outcomes of those events are uncorrelated in one’s epistemic probability assignment. Consider this toy example:

 

Suppose you have some background knowledge K and that your prior subjective probability function P, conditionalized on K, assigns non-negligible probability to only three possible worlds and assigns an equal probability to these: P(w₁|K) = P(w₂|K) = P(w₃|K) . In w₁ there is one big universe, a, and one small universe, d; in w₂ there is one big, b, and one small, e; and in w₃ there is one big, c, and one small, e. Now suppose you learn that you are in universe e. This rules out w₁. It thus gives you information about the big universe – it is now more likely to be either b or c than it was before you learnt that the little universe is e. That is, P("The big universe is b or c"|K&"The little universe is e") > P("The big universe is b or c"|K).

 

No assumption is made here about the universes being causally related. White presupposes that there is no such subjective probability function P, or that such a probability function must be irrational or unreasonable (independently of the exact nature of the various possible worlds under consideration). But that seems an implausible assumption, and no argument is provided for it.

            Third, White’s view that P(M|E’) > P(M) seems to commit him to denying this assumption. For how could E’ (which says that some universe is life-permitting) be probabilistically relevant to M unless the outcome of one universe-creating event x (namely that event, or one of those events, that created the life-permitting universe(s)) can be probabilistically relevant to the outcome of another y (namely one of those events that created the universes other than x)? If x gives absolutely no information about y, then there is no reason to think that because x resulted in a life-permitting universe, so did quite probably y too. So on this reasoning, we would have P(M|E’) = P(M). (This point connects back with the initial observation regarding the symmetry and the implausibility of thinking that because it is our universe that is life-permitting this gives less support for the multiverse hypothesis than if it had been some other universe instead that were life-permitting.)

            I conclude that White’s argument against the view that fine-tuning lends some support to the multiverse hypothesis fails, and so do consequently Phil Dowe’s and Ian Hacking’s (the latter failing on additional grounds as well, as described in the preceding section).

Surprising vs. unsurprising improbable events

If, then, the fact that our universe is life-permitting does give support to the multiverse hypothesis, i.e. P(M|E) > P(M), it follows from Bayes’ theorem that P(E|M) > P(E). How can the existence of a multiverse make it more probable that this universe should be life-permitting? One may be tempted to say: By making it more likely that this universe should exist. The problem with this reply is that it would seem to equally validate the inference to many universes from any sort of universe whatever. For instance, let E* be the proposition that  is a universe that contains nothing but chaotic light rays. It seems wrong to think that P(M|E*) > P(M). Yet, if the only reason that P(E|M) > P(E) is that is more likely to exist if M is true, then an exactly analogous reason would support P(E*|M) > P(E*), and hence P(M|E*) > P(M). This presents the anthropic theorizer with a puzzle.

            Several prominent supporters of the anthropic argument for the multiverse hypothesis have sought to ground their argument in a distinction between events (or facts) that are surprising and those that are improbable but not surprising (e.g. John Leslie (Leslie 1989) and Peter van Inwagen (van Inwagen 1993)).[5] Suppose you toss a coin one hundred times and write down the results. Any particular sequence s is highly improbable (P(s) = 2^-100), yet most sequences are not surprising. If s contains roughly equally many heads and tails, and no clear pattern, then s is improbable and unsurprising. By contrast, if s consists of 100 heads, or of alternating heads and tails, or some other highly patterned outcome, then s is surprising. Or to take another example, if x wins a lottery with one billion tickets, this is said to be unsurprising ("someone had to win, it could just as well be x as anybody else. shrug."); whereas if there are three lotteries with a thousand tickets each, and x wins all three of them, this is surprising. We evidently have some intuitive concept of what it is for an outcome to be surprising in cases like these.

            The idea, then, is that a fine-tuned universe is surprising in a sense in which a particular universe filled with only chaotic electromagnetic radiation would not have been. And that’s why we need to look for an explanation of fine-tuning but would not have had any reason to suppose there were an explanation for a light-filled universe. The two potential explanations for fine-tuning that typically are considered are the design hypothesis and the multiple universe hypothesis. An inference is then made that at least one of these hypotheses is quite likely true in light of available data, or at least more likely true than would have been the case if this universe had been a "boring" one containing only chaotic light. This is similar to the 100 coin flips example: an unsurprising outcome does not lead us to search for an explanation, while a run of 100 heads does cry out for explanation and gives at least some support to potential explanations such as the hypothesis that the coin flipping process was biased. Likewise in the lottery example. The same person winning the all three lotteries could make us suspect that the lottery had been rigged in the winner’s favor, especially if there were some independent evidence for this.

            A key assumption in this argument is that fine-tuning is indeed surprising. Is it? Some dismiss the possibility out of hand. For example, Stephen Jay Gould writes:

 

Any complex historical outcome – intelligent life on earth, for example – represents a summation of improbabilities and becomes therefore absurdly unlikely. But something has to happen, even if any particular "something" must stun us by its improbability. We could look at any outcome and say, "Ain’t it amazing. If the laws of nature had been set up a tad differently, we wouldn’t have this kind of universe at all." (Gould 1990, p. 183)

 

Peter van Inwagen mocks that way of thinking:

 

Some philosophers have argued that there is nothing in the fact that the universe is fine-tuned that should be the occasion for any surprise. After all (the objection runs), if a machine has dials, the dials have to be set some way, and any particular setting is as unlikely as any other. Since any setting of the dial is as unlikely as any other, there can be nothing more surprising about the actual setting of the dials, whatever it may be, than there would be about any possible setting of the dials if that possible setting were the actual setting. … This reasoning is sometimes combined with the point that if "our" numbers hadn’t been set into the cosmic dials, the equally improbable setting that did occur would have differed from the actual setting mainly in that there would have been no one there to wonder at its improbability. (van Inwagen 1993, pp. 134-5)

 

Opining that this "must be one of the most annoyingly obtuse arguments in the history of philosophy", van Inwagen asks us to consider the following analogy. Suppose you have to draw a straw from a bundle of 1,048,576 straws of different length. It has been decreed that unless you draw the shortest straw you will be instantly killed so that you don’t have time to realize that you didn’t draw the shortest straw. "Reluctantly – but you have no alternative – you draw a straw and are astonished to find yourself alive and holding the shortest straw. What should you conclude?" According to van Inwagen, only one conclusion is reasonable: that you did not draw the straw at random but that instead the situation was somehow rigged by an unknown benefactor to ensure that you got the shortest straw. The following argument to the contrary is dismissed as "silly":

 

Look, you had to draw some straw or other. Drawing the shortest was no more unlikely than drawing the 256,057th-shortest: the probability in either case was .000000954. But your drawing the 256,057th-shortest straw isn’t an outcome that would suggest a ‘set-up’ or would suggest the need for any sort of explanation, and, therefore, drawing the shortest shouldn’t suggest the need for an explanation either. The only real difference between the two cases is that you wouldn’t have been around to remark on the unlikelihood of drawing the 256,057th-shortest straw. (van Inwagen 1993, p. 135)

 

Given that the rigging hypothesis did not have too low a prior probability and given that there was only one straw lottery, it is hard to deny that this argument would indeed be silly. What we need to reflect about, though, is whether the example is analogous to our epistemic situation regarding fine-tuning.

            Erik Carlson and Erik Olsson (Carlson and Olsson 1998), criticizing van Inwagen’s argument, argue that there are three points of disanalogy between van Inwagen’s straw lottery and fine-tuning. First, they note that whether we would be willing to accept the "unknown benefactor" explanation after drawing the shortest straw depends on our prior probability of there being an unknown benefactor with the means to rig the lottery. If the prior probability is sufficiently tiny – given certain background beliefs it may be very hard to see how the straw lottery could be rigged – we would not end up believing in the unknown benefactor hypothesis. Obviously, the same applies to the fine-tuning argument: if the prior probability of a multiverse is small enough then we won’t accept that hypothesis even after discovering a high degree of fine-tuning in our universe. I think the multiverse supporter can grant this and argue that the prior probability of a multiverse is not too small. Exactly how small it can be for us still to end up accepting the multiverse hypothesis depends on both how extreme the fine-tuning is and what alternative explanations are available. If there is plenty of fine-tuning, and the only alternative explanation on the table is the design hypothesis, and if that hypothesis is assigned a much lower prior probability than the multiverse hypothesis, then the argument for the multiverse hypothesis would be vindicated. We don’t need to commit ourselves to these assumptions; and in any case, different people might have different prior probabilities. What we are primarily concerned with here is to determine whether fine-tuning is in a relevant sense a surprising improbable event, and whether taking fine-tuning into account should substantially increase our credence in the multiverse hypothesis and/or the design hypothesis, not what the absolute magnitude of our credence in those hypotheses should be. Carlson and Olsson’s first point is granted but it doesn’t have any bite. van Inwagen never claimed that his straw lottery example could settle the question of what the prior probabilities should be.

            Carlson and Olsson second point would be more damaging for van Inwagen, if it weren’t incorrect. They claim that there is a fundamental disanalogy in that we understand at least roughly what the causal mechanisms are by which intelligent life evolved from inorganic matter whereas no such knowledge is assumed regarding the causal chain of events that led you to draw the shortest straw. To make the lottery more closely analogous to the fine-tuning, we should therefore add to the description of the lottery example that at least the proximate causes of your drawing the shortest straw are known. Carlson and Olsson then note that:

 

In such a straw lottery, our intuitive reluctance to accept the single-drawing-plus-chance hypothesis is, we think, considerably diminished. Suppose that we can give a detailed causal explanation of why you drew the shortest straw, starting from the state of the world twenty-four hours before the drawing. A crucial link in this explanation is the fact that you had exactly two pints of Guinness on the night before the lottery. … Would you, in light of this explanation of your drawing the shortest straw, conclude that, unless there have been a great many straw lotteries, somebody intentionally caused you to drink two pints of Guinness in order to ensure that you draw the shortest straw? … To us, this conclusion does not seem very reasonable. (Carlson and Olsson 1998, pp. 271-2)

 

The objection strikes me as unfair. Obviously, if you knew that your choosing the shortest straw depended crucially and sensitively on your precise choice of beverage the night before, you would feel disinclined to accept the rigging hypothesis. That much is right. But this disinclination is fully accounted for by the fact that it is tremendously hard to see, under such circumstances, how anybody could have rigged the lottery. If we knew that successful rigging required predicting in detail such a long and tenuous causal chain of events, we could well conclude that the prior probability of rigging was negligible. For that reason, surviving the lottery would not make us believe the rigging hypothesis. We can see that it is this – rather than our understanding of the proximate causes per se – that defeats the argument for rigging, by considering the following variant of van Inwagen’s example. Suppose that the straws are scattered over a vast area. Each straw has one railway track leading up to it, all the tracks starting from the same station. When you pick the shortest straw, we now have a causal explanation that can stretch far back in time: you picked it because it was at the destination point of a long journey along a track that did not branch. How long the track was makes no difference to how willing we are to believe in the rigging hypothesis. What matters is only whether we think there is some plausibility to the idea that an unknown benefactor could have put us on the right track to begin with. So contrary to what Carlson and Olsson imply, what is relevant is not the known backward length of the causal chain, but whether that chain would have been sufficiently predictable by the hypothetical benefactor to give a sufficient prior probability to the hypothesis that she rigged the lottery. Needless to say, the designer referred to in the deign hypothesis is typically assumed to have superhuman epistemic capacities. It is not at all farfetched to suppose that if there were a cosmic designer, she would have been able to anticipate which boundary conditions of the universe were likely to lead to the evolution of life. We should therefore reject Carlson and Olsson’s second objection against van Inwagen’s analogy.

            The third alleged point of disanalogy is somewhat subtler. Carlson and Olsson discuss it in the context of refuting certain claims by Arnold Zuboff (Zuboff 1991) and it is not clear how much weight they place on it as an objection against van Inwagen. It’s nonetheless worth mentioning. The idea, so far as I can make it out, is that the reason why your existing after the straw lottery is surprising, is related to the fact that you existed before the straw lottery. You could have antecedently contemplated your survival as one of a variety of possible outcomes. In the case of fine-tuning, by contrast, your existing (or intelligent life existing) is not an outcome which could have been contemplated prior to its obtaining.

 

For conceptual reasons, it is impossible that you know in advance that your existence lottery is going to take place. Likewise, it is conceptually impossible that you make any ex ante specification of any possible outcome of this lottery. … The existence of a cosmos suitable for life does not seem to be a coincidence for anybody; nobody was ever able to specify this outcome of the cosmos lottery, independently of its actually being the actual outcome. (Carlson and Olsson 1998, p. 268)

 

This might look like a token of the "annoyingly obtuse" reasoning that van Inwagen thought to refute through his straw lottery example. All the same, there is a disanalogy between the two cases: nobody could have contemplated the existence of intelligent life unless intelligent life existed, whereas someone (even the person immediately involved) could have thought about drawing the shortest straw before drawing it. But the question is whether this difference is relevant. Again it is useful to cook up a variant of van Inwagen’s example:

 

Suppose that in an otherwise lifeless universe there is a big bunch of straws and a simple (non-cognitive, non-conscious) automaton about to randomly select one of the straws. There is also kind of "incubator" in which one person rests in an unconscious state; we can suppose she has been unconscious since the beginning of time. The automaton is set up in such a way that the person in the incubator will be woken if and only if the automaton picks the shortest straw. You wake up in the incubator. After examining your surroundings and learning about how the experiment was set up, you begin to wonder about whether there were anything surprising about the fact that the shortest straw was drawn.

 

This example shares with the fine-tuning case the feature that nobody would have been there to contemplate anything if the "special" outcome had failed to obtain. So what should we say about this case? In order for Carlson and Olsson’s criticism to work, we would have to say that the person waking up in the incubator should not think that there is anything surprising at all about the shortest straw having been selected. van Inwagen would most probably simply deny that that would be the correct attitude. For what it’s worth, my intuition in this instance sides with Inwagen, although this case is perhaps less obvious than van Inwagen’s original straw lottery where the subject had a life before the lottery.

It would be nice to have an independent account of what makes an event or a fact surprising. We could then apply the general account to the straw lotteries or directly to fine-tuning, and see what follows. Let us therefore review what efforts have been made to develop such an account of surprisingness. (I'm heavily indebted here to fine literature-survey and discussion in Neil Manson's doctoral thesis (Manson 1998).) To anticipate the upshot: I will argue that these represent a dead end as far as anthropic reasoning is concerned. From this we will learn that the strategy of some anthropic theorizers to base their case on an appeal to what is surprising is ultimately of very limited utility: the strategy is grounded on intuitions that are not any more obvious or secure than the thesis which they are employed to support. This may seem disappointing, but in fact it clears the path for a better understanding what is required to support anthropic reasoning.

The following remark by F. P. Ramsey is pertinent to the goal of determining what distinguishes surprising improbable events from unsurprising improbable events:

 

What we mean by an event not being a coincidence, or not being due to chance, is that if we came to know it, it would make us no longer regard our system as satisfactory, although on our system the event may be no more improbable than any alternative. Thus 1,000 heads running would not be due to chance; i.e. if we observed it we should change our system of chances for that penny. (Ramsey 1990, p. 106)

 

This looks like promising beginning. It seems to fit the other example considered near the beginning of this section: one person winning three lotteries with a thousand tickets could make us suspect foul play, whereas one person winning a billion-ticket lottery would not in general have any tendency do so. Or ponder the case of a monkey typing out the sequence "Give me a banana!". This is surprising and it makes us change our belief that the monkey types out a random sequence. We would think that maybe the monkey had been trained to type that specific sequence, or maybe that the typewriter was rigged; but the chance hypothesis is disconfirmed. By contrast, if the monkey types out "r78o479024io; jl;", this is unsurprising and does not challenge our assumptions about the setup. So far so good.

What Ramsey’s suggestion does not tell us what it is about events such as the monkey’s typing a meaningful sentence or the run of 1000 heads that makes us change our mind about the system of chances. We need to know that if the suggestion is to throw any light on the fine-tuning case. For the problem there is precisely that it is not immediately clear – lest the question be begged – whether we ought to change our system and find some alternative explanation or be satisfied with letting chance pay the bill, that is, in Ramsey’s terminology, regarding fine-tuning as a coincidence. Ramsey’s suggestion is thus insufficient for the present purpose.

Paul Horwich takes the analysis further. He proposes the following as a necessary condition for the truth of a statement E being surprising:

 

[T]he truth of E is surprising only if the supposed circumstances C, which made E seem improbable, are themselves substantially diminished in probability by the truth of E…and if there is some initially implausible (but not widely implausible) alternative view K about the circumstances, relative to which E would be highly probable. (Horwich 1982, p. 101)

 

If we combine this with the condition that "our beliefs C are such as to give rise to ", we get what Horwich thinks is a necessary and sufficient condition for the truth of a statement being surprising. We can sum this up by saying that the truth of E is surprising iff the following holds:

 

(i)        

(ii)       

(iii)      

(iv)       P(K) is small but not too small

 

            Several authors who think that fine-tuning cries out for explanation endorse views that are similar to Horwich’s (Manson 1989). For instance, Peter van Inwagen writes:

 

Suppose there is a certain fact that has no known explanation; suppose that one can think of a possible explanation of that fact, an explanation that (if only it were true) would be a very good explanation; then it is wrong to say that that event stands in no more need of an explanation than an otherwise similar event for which no such explanation is available. (van Inwagen 1993, p. 135)

 

And John Leslie:

 

A chief (or the only?) reason for thinking that something stands in [special need for explanation], i.e. for justifiable reluctance to dismiss it as how things just happen to be, is that one in fact glimpses some tidy way in which it might be explained. (Leslie 1989, p. 10)

 

D.J. Bartholomew also appears to support a similar principle (Bartholomew 1984). Horwich’s analysis provides a reasonably good explication of these ideas.

George Schlesinger (Schlesinger 1991) has criticized Horwich’s analysis, arguing that the availability of a tidy explanation is not necessary for an event being surprising. Schlesinger asks us to consider the case of a tornado that touches down in three different places, destroying one house in each place. We are surprised to learn that these houses belonged to the same person and that they are the only buildings that this misfortunate capitalist owned. Yet no neat explanation suggests itself. Indeed, it seems to be because we can see no tidy explanation (other than the chance hypothesis) that this phenomenon would be so surprising. So if we let E to be the event that the tornado destroys the only three buildings that some person owns and destroys nothing else, and C the chance hypothesis, then (ii) - (iv) are not satisfied. According to Horwich’s analysis, E is not surprising – which is counterintuitive.

            Surprise being ultimately a psychological matter, we should perhaps not expect any simple definition to perfectly capture all the cases where we would feel surprised. But maybe Horwich has provided at least a sufficient condition for when we ought to feel surprised? Let’s run with this for a second and see what happens when we apply his analysis to fine-tuning. In order to do this we need to determine the probabilities referred to in (i)-(iv). Let’s grant that the prior probability of fine-tuning (E) is very small, . Further, anthropic theorizers maintain that E makes the chance hypothesis substantially less probable than it would have been without conditionalizing E, so let’s suppose that [6]. Let K be a multiverse hypothesis. In order to have , it might be necessary to think of K as more specific than the proposition that there is some multiverse; we may have to define K as the proposition that there is a "suitable" multiverse (i.e. one such that  is satisfied). But let us suppose that even such a strengthened multiverse hypothesis has a prior probability that is not "too small". If we make these assumptions then Horwich’s four conditions are satisfied, and the truth of E would consequently be surprising. This is the result that the anthropic theorizer would like to see.

            Unfortunately, we can construct a similar line of assumptions to show that any other possible universe would have been equally surprising. Let E^# be the proposition that  has some particular boring character. For instance, we can let E^# say that  is a universe which consists of nothing but such-and-such a pattern of electromagnetic radiation. We then have . We can let K be the same as before. Now, if we suppose that  and  then the truth of E^# will be classified as surprising. This is counterintuitive, and if it were true that every possible universe would be just as surprising as any other then fine-tuning being surprising can surely not be what legitimizes the inference from fine-tuning to the multiverse hypothesis. We must therefore deny either  or  (or both). At the same time, if the truth of E is to be surprising, we must maintain that  and . This means that the anthropic theorizer wishing to ground her argument in an appeal to surprise must treat E^# differently from E as regards these conditional probabilities. It may be indeed be correct to do that. But what is the justification? Whatever is it, it cannot be that the truth of E is surprising whereas the truth of E^# is not. For although that might be true, to simply assume that would be to make the argument circular.

The appeal to the surprisingness of E is therefore quite ineffective. In order to give the appeal any force, it needs to be backed up by some argument for the claim that: ,  but not both  and . But suppose we had such an argument. We could then sidestep considerations about surprisingness altogether. For it follows already from , , and P(K) being "not too small", that , i.e. that fine-tuning is strong evidence for the multiverse hypothesis. (To see this, simply plug the values into Bayes’ formula, .)

To make progress beyond this point, it is imperative to abandon vague talk of what makes events surprising and focus explicitly on the core issue, which is to determine the conditional probability of the multiverse hypothesis/chance hypothesis/design hypothesis given the evidence we have. If we figure out how to think about these conditional probabilities then we can hopefully use this insight to sort out the quandary about whether fine-tuning should be regarded as surprising. At any rate, that quandary becomes much less important if we have a direct route to assigning probabilities to the relevant hypotheses that skips the detour through the dark netherworld of amazement and surprise. This is what we shall now do.

Observational selection effects

I suggest that the only way to get a plausible model of how to reason from fine-tuning is to integrate it into a general theory which takes explicit account of observational selection effects. This section will outline parts of such a theory. Later chapters will expand and support themes that are merely alluded to here. A theory of observational selection effects has applications in many domains. In this section we focus on applications in cosmology.

            As before, let "" rigidly denote our universe. We know some things K about  (it’s life-permitting; it contains the Eiffel tower; it’s quite big etc.). Let h_M be the multiverse hypothesis; let h_D be the design hypothesis; and let h_C be the chance-hypothesis. I suggest that in order to determine what values to assign to the conditional probabilities P(h_M|K), P(h_D|K), and P(h_C|K), we need to take account of the observational selection effects through which our evidence about the world was filtered. Recall the example from the introduction – catching a 20 cm long fish with an apparatus that can only catch fish of precisely that length – this limitation of the sampling apparatus obviously needs to be taken into account when trying to guess the size-distribution of the lake’s fish population. Similarly for the pollster who samples from an unrepresentative subset of the electorate, or the economist who seeks to estimate the average growth rate of startups in their first year by looking only at companies listed in the Yellow pages. The data obtained through these methods is not necessarily worthless, but we have to take care to correct as best we can for the known selection effects that are involved. A moment’s reflection reveals that analogous selection effects may have biased the data we have about the large scale structure of cosmos. These include observational selection effects: biases that are due to the fact that only those parts of the whole that have a certain physical proximity to parts where observers exist are observed.

            We shall now consider how we can model these observational selection effects. Suppose that you are an angel. So far nothing physical exists, but six days ago God told you that he was going away for a week to create a cosmos. He might create either a single universe or a multiverse, and let’s say your prior probabilities for these two hypotheses are about 50%. Now a messenger arrives and informs you that God’s work is completed. The messenger tells you that universe  exists but does not say whether there are other universes in addition. Should you think that God created a multiverse or only ? To answer this, we need to know something more about the situation. Consider two possible specifications of what happened:

 

Case 1. The messenger decided to travel to realm of physical existence and look at the universe or one of the universes that God had created. This universe was , and this is what he reports to you.

Case 2. The messenger decided to find out whether God created . So he travels to the realm of physical existence and looks until he finds , and reports this back to you.

 

In Case 1, the messenger’s tidings do not in general give you any reason to believe h_M. He was bound to bring back news about some universe, and the fact that he tells you about  rather than some other universe is not significant, unless  has some special feature F. (More on this proviso shortly.)

In Case 2 on the other hand, the fact that the messenger tells you that  exists is evidence for h_M. If the messenger selected  randomly from the class of all possible universes, or from some sizeable subclass thereof (for example only big bang universes with the same laws of nature as in our universe, or only universes which contain more good than evil), then the finding that God created  suggests that God created many universes.

            Our actual epistemic situation is not analogous to the angel’s in Case 2. It is not as if we first randomly selected  from a class containing both actual and non-actual possible universes and then discovered that – lo and behold! –  actually exists. The fact that we know whether  exists surely has everything to do with it actually existing and we being among its inhabitants. There is an observational selection effect amounting to the following: direct observation occurs only of universes that actually exist. Case 1 comes closer to modeling our epistemic situation in this respect, since it mirrors this selection effect.

            However, Case 1 is still an inadequate model because it overlooks another observational effect. The messenger could have retrieved information about any of the actual universes, and the angel could have found out about some universe  that doesn’t contain any observers. If there are no angels, gods or heavenly messengers, however, then universes that don’t contain observers are not observed. Assuming the absence of extramundane observers, the selection effect restricts what is observed not only to the extent that non-actual universes are not observed but actual universes that don’t contain any observers are also not observed. This needs to be reflected in our model. If we want to continue to use the creation story, we therefore need to modify it as follows:

 

Case 3. The messenger decided to travel to the realm of physical existence and look for some universe that contains observers. He found , and reports this back to you.

 

            Does this provide you with any evidence for h_M? It depends. If you knew (call this Case 3a) that God had set out to create at least one observer-containing universe, then the tiding that  is actual does not give any support to h_M (unless you know that  has some special feature). Because then you were guaranteed to learn about the existence of some observer-containing universe or other and learning that it is  does not give any more evidence for h_M than if you had learnt about some other universe instead. The messenger’s tidings T contain no relevant new information; the probably you assign to h_M remains unchanged. In Case 3a, therefore, P(h_M|T) = P(h_M).

            But there is second way of specifying Case 3. Suppose (Case 3b) that God did not set out especially to create at least one observer-containing universe, and that for any universe that He created there was a only a fairly small chance that it would be observer-containing. In this case, when the messenger reports that God created the observer-containing universe , you get evidence that favors h_M. For it is more probable on h_M than it is on ¬ h_M that one or more observer-containing universes should exist (one of which the messenger was then bound to bring you news about). Here, we therefore have P(h_M|T) > P(h_M).

What is grounding T’s support for h_M? I think it is best answered not by saying that T makes it more probable that  should exist, but rather that T makes it more probable that at least one observer-containing universe should exist. It is nonetheless true that h_M makes it more probable that  should exist. But this is not by itself the reason why h_M is to be preferred given our knowledge of the existence of . If it were, then since the same reason operates in Case 3a, we would have to have concluded that h_M were favored in that case as well. For even though it was guaranteed in Case 3a that some observer-containing universe would exist, it was not guaranteed that it would be . In Case 3a as well as in Case 3b, the existence of  was made more likely by h_M than by ¬ h_M. If this should not lead us to favor h_M in Case 3a then the fact that the existence of  is made more likely by h_M cannot be the whole story about why h_M is to be preferred in Case 3b.

So what is the whole story about this? This will become clearer as we proceed, but we can give at least the outlines now. In subsequent chapters we shall fill in important details and see some arguments for the claims we make here.

            In a nutshell: although h_M makes it more probable that  should exist, h_M also makes it more probable that there are other observer-containing universes. And the greater the number of observer-containing universes, the smaller the probability that we should observe any particular one of them. These two effects balance each other. We can get some intuitive grasp of this if we consider a two-step procedure. Suppose the messenger first tells you that some observer-containing universe x exists. This rules out all hypotheses on which there would be no such universes; it counts against hypotheses on which it would be very unlikely that there were any observer-containing universes; and it favors hypotheses on which it would be very likely or certain that there were one or more observer-containing universes. In the second step, the messenger tells you that x = . This would not change your beliefs as to how many observer-containing universes there are (assuming you don’t think there is anything special about ). One might say that if God were equally likely to create any universe, then the probability that  should exist is proportional to the number of universes God created. True. But the full evidence you have is not only that  exists but also that the messenger told you about . If the messenger selected the universe he reports randomly from the class of all actual observer-containing universes, then the probability that he would select , given that  is an actual observer-containing universe, is inversely proportional to the number of actual observer-containing universes. The messenger’s report therefore does not allow you to discriminate between general hypotheses[7] that imply that at least one observer-containing universe exists. In our actual situation our knowledge is not mediated by a messenger; but the suggestion is that the data we get about the world are subjected to observational selection effects that mimic the reporting biases present in Case 3.

            When stating that the finding that  exists does not give us reason to think that there are many rather than few observer-containing universes, we have kept inserting the proviso that  not be "special". This is an essential qualification, for there clearly are some features such that if we know that  has them then finding that  exists would give support to claim that there are a vast number of observer-containing universes. For instance, if you know that  is a universe in which a message is inscribed in every rock, in the distribution of fixed stars seen from any life-bearing planet, and in the microstructure of common crystal lattices, spelling: "God created this universe. He also created many other universes." – then the fact that the messenger tells you that  exists can obviously give you some reason to think that there are many universes. In our actual universe, if we were to find inscriptions that we were convinced could only have been created by a divine being then this would count as support for whatever these inscriptions asserted (the degree of support being qualified by the strength of our conviction that the deity was being honest). Leaving aside such theological scenarios, there are much more humdrum features our universe might have that could make it special in the sense intended here. It may be, for example, that the physics of our universe is such as to suggest a physical theory (because it’s the simplest, most elegant theory that fits the facts) which entails the existence of vast numbers of observer-containing universes.

            Fine-tuning may well be a "special" feature. This is so because fine-tuning seems to indicate that there is no simple, elegant theory which entails (or gives a high probability to) the existence our universe alone but not the existence of other universes. If it were to turn out, present appearances notwithstanding, that there is such a theory then our universe is not special. But in that case there would not be any reason to think that our universe really is fine-tuned. For if a simple theory entails that precisely this universe should exist, then one could plausibly assert that no other boundary conditions than those implied by that theory are physically possible; and hence that physical constants and initial conditions could not have been different than they are – thus no fine-tuning. However, assuming that every theory fitting the facts and entailing that there is only one universe is a very ad hoc one and involving many free parameters – as fine-tuning advocates argue – then the fine-tuning of our universe is a special feature that gives support to the hypothesis that there are many universes. There is nothing mysterious about this. Preferring simple theories that fit the facts to complicated ad hoc ones is just standard scientific practice, and cosmologists that work with multiverse theories are presumably pursuing that inquiry because they think that multiverse theories represent a promising route forward to neat theories that are empirically adequate.

            We can now answer the questions asked at the beginning of this chapter: Does fine-tuning cry out for explanation? Does it give support to the multiverse hypothesis? Beginning with the latter question, we should say: Yes, to the extent that multiverse theories are simpler, more elegant (and therefore claming a higher prior probability) than any rival theories that are compatible with what we observe. In order to be more precise about the magnitude of support, we need to determine the conditional probability that a multiverse theory gives to the observations we make. We have said something about how such conditional probabilities are determined: The conditional probability is greater – ceteris paribus – the greater the probability that the multiverse theory gives to the existence of a universe exactly like ours; it is smaller – ceteris paribus – the greater the number of observer-containing universes it entails. These two factors balance each other to the effect that if we are comparing various multiverse theories then what matters, generally speaking, is the likelihood they assign to at least some observer-containing universe existing; if two multiverse theories both do that, then there is no general reason to favor or disfavor the one that entails the larger number of observer-containing universes. All this will become clearer in subsequent chapters where the current hand-waving will be replaced by mathematically precise models.

            The answer to the question whether fine-tuning cries out for explanation follows from this. If something’s "crying out for explanation" means that it would be unsatisfactory to leave it unexplained or to dismiss it as a chance event, then fine-tuning cries out for explanation at least to the extent that we have reason to believe in some theory that would explain it. At the present, multiverse theories may look like reasonably promising candidates. For the theologically inclined, the Creator-hypothesis is also a candidate. And there remains the possibility that fine-tuning could turn out to be an illusion – if some neat single-universe theory that fits the data is discovered in the future.[8]

            Finally, we may also ask whether there is anything surprising about our observation of fine-tuning. Let’s assume, as the question presupposes, that the universe really is fine-tuned, in the sense that there is no neat single-universe theory that fits the data (but not in a sense that excludes our universe being one in an ensemble that is itself not fine-tuned). Is such fine-tuning surprising on the chance-hypothesis? It is, per assumption, a low-probability event if the chance-hypothesis is true; and it would tend to disconfirm the chance-hypothesis if there is some other hypothesis with reasonably high prior probability that assigns a high conditional probability to fine-tuning. For it to be a surprising event then (using Horwich’s analysis) there has to be some alternative to the chance-hypothesis that meets conditions (iii) and (iv). Many would hold that the design hypothesis satisfies these criteria. But if we rule out the design hypothesis, does the multiverse hypothesis fit the bill? We can suppose, for the sake of the argument at least, that the prior probability of the multiverse hypothesis is not too low, so that (iv) is satisfied. The sticky point is condition (iii), which requires that . According to the discussion above, the conditional probability of us observing a fine-tuned universe is greater given a suitable multiverse than given the existence of a single random universe. If the multiverse hypothesis is of a suitable kind – such that it entails (or makes it highly likely) that at least one observer-containing universe exists – then the conditional probability, given that hypothesis, of us observing an observer-containing universe should be set equal (or very close) to one. It then comes down to whether on this hypothesis representative[9] observer-containing universes would be fine-tuned.[10] If they would, then it follows that this multiverse hypothesis should be taken to give a very high likelihood to our observing a fine-tuned universe; so Horwich’s condition (iii) would be satisfied, and our observing fine-tuning would count as a surprising event. If, on the other hand, representative observer-containing universes in the multiverse would not be fine-tuned, then condition (iii) would not be satisfied, and the fine-tuning would not qualify as surprising.[11]

            Note that in answering the question whether fine-tuning was surprising, we focused on E’ (the statement that there is a fine-tuned universe) rather than E (the statement that  is fine-tuned). I suggest that what is primarily surprising is E’, and E is surprising only in the indirect sense of implying E’. If E is independently surprising, then on Horwich’s analysis, it has to be so owing to some other alternative[12] to the chance-hypothesis than the multiverse hypothesis, since it is not the case that . But I find it quite intuitive that what would be surprising on the chance-hypothesis is not that this universe (understood rigidly) should be fine-tuned but rather that there should be a fine-tuned universe at all if there is only one universe in total and fine-tuning was highly improbable.

Conclusions

It may be useful to summarize the main findings of this chapter. We set out to investigate whether fine-tuning needs explaining and whether it gives support to the multiverse hypothesis. We found that:

·        There is an easy part of the answer: Leaving fine-tuning unexplained is epistemically unsatisfactory to the extent that it involves accepting complicated, inelegant theories with many free parameters. If a neater theory can account for available data it is to be preferred. This is just an instance of the general methodological principle that one should prefer simpler theories, and it has nothing to do with fine-tuning as such (i.e. this point is unrelated to the fact that observers would not have existed if boundary conditions had been slightly different).

·        Ian Hacking’s argument that multiverse theories such as Wheeler’s oscillating universe model cannot receive any support from fine-tuning data, while multiverse theories such as the one Hacking ascribes to Brandon Carter can receive such support, is flawed. So are the more recent arguments by Roger White and Phil Dowe purporting to show that multiverse theories tout court would not be supported by fine-tuning.

·        Those who think fine-tuning gives some support to the multiverse hypothesis have typically tried to argue for this by appealing to the surprisingness of fine-tuning. We examined van Inwagen’s straw lottery example, refuted some objections by Carlson and Olsson, and suggested a variant of Inwagen’s example that is more closely analogous to our epistemic situation regarding fine-tuning. In this variant the verdict seems to favor the multiverse advocates, although there appears to be room for opposing intuitions. In order to give the idea that an appeal to the surprisingness of fine-tuning could settle the issue a full run for its money, we considered Paul Horwich’s analysis of what makes the truth of a statement surprising. This analysis seems to provide the best available explication of what multiverse advocates mean when they talk about surprise. It was found, however, that applying Horwich’s analysis to the fine-tuning situation did not suffice to settle the issue of whether fine-tuning is surprising. We concluded that in order to determine whether fine-tuning cries out for explanation or gives support for the multiverse hypothesis, it is not enough to appeal to the surprisingness or amazingness of fine-tuning. One must to drill deeper.

·        What is needed is a way of determining the conditional probability P(E|h_M). I suggested that in order to get this right, it is essential to take into account observational selection effects. We created an informal model of how to think about such effects in the context of fine-tuning. Some of the preliminary (not yet conclusively argued for) results of this are as follows:

·        Fine-tuning favors (other things equal) hypotheses on which it is likely that one or more observer-containing universes exist over hypotheses on which it is unlikely that even one observer-containing universe should exist.

·        If two competing general hypotheses each imply that there is at least some observer-containing universe, but one of them implies a greater number of observer-containing universes, then fine-tuning is not typically a reason to favor the latter (other things equal). The number of observerless universes implied is typically also not relevant.

·        Although P(E|h_M) may be much closer to zero than to one, this conditional probability could nonetheless well be large enough (after taking observational selection effects into account) for E to favor the multiverse hypothesis.

·        The answer to the "tricky part" of the question about whether fine-tuning needs explanation or supports the multiverse hypothesis: Yes, there is something about fine-tuning as such that adds to the need for explanation and to the support for the multiverse hypothesis over and above the general principle that simplicity is epistemically attractive. The reason for this is twofold. First, the availability of a potential rival explanation for why the universe should be observer-containing. The design hypothesis, presumably, can more plausibly be invoked to explain a world consisting of an observer-containing universe than to explain a world consisting of a boring non-observer-containing universe. Second (theology apart), the capacity of the multiverse hypothesis to give a high likelihood to E (and thereby in some sense to explain E), and to gain support from E, depends essentially on observational selection effects. Fine-tuning is therefore not just like any other way in which a theory may require a delicate setting of various free parameters to fit the data. The presumption that observers would not be so likely to exist if the universe were not fine-tuned is essential. For that means that if a multiverse theory implies that there is an ensemble of universes, only a few of which are fine-tuned, what the theory predicts that we should observe is still one of those exceptional fine-tuned universes. The observational selection effect enables the theory to give our observing a fine-tuned universe a high conditional probability even though such a universe may be very atypical of the cosmos as a whole. If there were no observational selection effect restricting our observation to an atypical proper part of cosmos then postulating a bigger cosmos would not in general incur a greater likelihood of us observing a particular feature. (It may make it more likely that that feature should be instantiated somewhere or other, but it would also make it less likely that we should happen to be at any particular place where it was instantiated.) Fine-tuning, therefore, involves issues additional to the ones common to all forms of scientific explanation and inference.

·        On Horwich’s analysis of what makes the truth of a statement surprising, it would be surprising against the background of the chance-hypothesis that only one universe existed and it happened to be fine-tuned. By contrast, that this universe should be fine-tuned would not contain any additional surprise factor (unless one thought that the design hypothesis could furnish an explanation for this datum satisfying Horwich’s condition (iii) and (iv)).

CHAPTER 3: OBSERVATIONAL SELECTION EFFECTS AND THE ANTHROPIC PRINCIPLE

In chapter 2 we have seen how observational selection effects are relevant in assessing the implications of cosmological fine-tuning. We outlined of a model for how such effects modulate the conditional probability of us making certain observations given certain hypotheses about the large-scale structure of cosmos. The general idea that observational selection effects need to be taken into account in cosmological theorizing has been recognized by several authors, and there have been many attempts to express this idea under the rubric of "the anthropic principle". None of these attempts, however, quite hits the mark – some don’t even seem to know what they are aiming for. The first section of this chapter reviews some of the more helpful formulations of the anthropic principle found in the literature, and considers how far these can take us. Section two briefly discusses a set of very different "anthropic principles" and explains why they are misguided or at least irrelevant for present purposes. There is plenty of confusion about what the anthropic principle is and about its epistemological status. It is essential to clear this up and to distinguish the versions that I am interested in. Since a main thrust of this dissertation is that anthropic reasoning deserves serious attention, I want to be explicit about some associated ideas that I’m not endorsing. The third section continues where the first section left off. Arguing that formulations found in the literature are inadequate, I propose a simple but (as later chapters will show) surprisingly powerful methodological principle, which I dub the Self-Sampling Assumption.

The anthropic principle as expressing an observational selection effect

The term "anthropic principle" was coined by Brandon Carter. In a paper of 1974, he defined it as

 

… what we can expect to observe must be restricted by the conditions necessary for the our presence as observers. (Carter 1974, p. 126)

 

Carter’s concept of the anthropic principle, as evidenced by the uses to which he put it, is appropriate and useful, but his definitions and explanations of it are rather vague. While Carter himself was never in any doubt about how to understand and apply the principle, he did not explain it in a philosophically transparent enough manner to enable all his readers to do the same.

            The trouble starts with the name. Anthropic reasoning has nothing in particular to do with Homo sapiens. Calling the principle ‘anthropic’ is therefore misleading and has indeed misled some authors (e.g. Gould 1985, Worrall 1996, Gale 1981). Carter regrets not using a different name (Carter 1983). He suggests that maybe "the psychocentric principle", "the cognizability principle" or "the observer self-selection principle" would have been better. It is probably too late for terminological reform, but emphasizing that the anthropic principle concerns intelligent observers in general and not specifically human observers should be enough to prevent misunderstandings on this point.

            Carter introduced two versions of the anthropic principle, a strong version (SAP) and a weak (WAP). He defined the WAP thus:

 

… we must be prepared to take account of the fact that our location in the universe is necessarily privileged to the extent of being compatible with our existence as observers. (p. 127)

 

SAP states that:

 

… the Universe (and hence the fundamental parameters on which it depends) must be such as to admit the creation of observers within it at some stage. (p. 129)

 

            Carter’s formulations have been attacked for being mere tautologies (and therefore incapable of doing any interesting explanatory work whatever), and for being widely speculative (and lacking any empirical support). Often WAP is accused of the former and SAP of the latter. I think we have to admit that both these readings are possible, since WAP and SAP as stated are very vague. WAP says that we have to "be prepared to take into account" the fact that our location is privileged, but it does not specify how we are to take account of that fact. SAP says that the universe "must" admit the creation of observers, but it does not specify the force of this "must". We get a very different meanings depending how we interpret the "must". Does it merely serve to underline an entailment of available data ("the universe must be life-admitting – present evidence about our existence implies that!")? Or is the "must" instead to be understood in some stronger sense, for example as alleging some kind of prior metaphysical or theological necessity? On the former alternative, the principle is indisputably true; but then the difficulty is to explain how this trivial statement can be useful or important. On the second alternative, we can see how it could be contentful (provided we an make sense of the intended notion of necessity), the difficulty being to provide some reason for why we should believe it.

            John Leslie (Leslie 1989) argues that AP, WAP and SAP can all be understood as tautologies and that the difference between them is often purely verbal. In Leslie’s explication, AP simply says that:

 

Any intelligent living beings that there are can find themselves only where intelligent life is possible. (Leslie 1989, p. 128)

 

WAP then says that, within a universe, observers find themselves only at spatiotemporal locations where observers are possible. SAP states that observers find themselves only in universes that allow observers to exist. "Universes" means roughly: huge spacetime regions that might be more or less causally disconnected from other spacetime regions. Since the definition of a universe is not sharp, nor is the distinction between WAP and SAP. WAP talks about where within a life-permitting universe we should expect to find ourselves, while SAP talks about in what kind of universe in an ensemble of universes we should expect to find ourselves. On this interpretation the two principles are fundamentally similar, differing only in scope.

            For completeness, we may also mention Leslie’s (Leslie 1989) "Superweak Anthropic Principle", which states that:

 

If intelligent life’s emergence, NO MATTER HOW HOSPITABLE THE ENVIRONMENT, always involves very improbable happenings, then any intelligent living beings that there are evolved where such improbable happenings happened." (Leslie 1989, p. 132; emphasis and capitals as in the original).

 

The implication, as Michael Hart (Hart 1982) has stressed, is that we shouldn’t assume that the evolution of life on an earth-like planet might not well be very extremely improbable. Provided there are enough Earth-like planets, as there may well be in an infinite universe, then even a chance lower than 1 in 10^3,000 would be enough to ensure (i.e. give an arbitrarily great probability to the proposition) that life would evolve somewhere[13]. Naturally, what we would observe would be one of the rare planets were such an improbable chance-event had occurred. The Superweak Anthropic Principle can be seen as one particular application of WAP. It doesn’t add anything to what is already contained in Carter’s principles.

            The question that immediately arises is: hasn’t Leslie trivialized anthropic reasoning with this definition of AP? – Not necessarily. Whereas the principles he defines are tautologies, the invocation of them to do explanatory work is dependent on nontrivial assumptions about the world. Rather than the truth of AP being problematic, its applicability is problematic. That is, it is problematic whether the world is such that AP can play a part in interesting explanations and predictions. For example, the anthropic explanation of fine-tuning requires the existence of an ensemble of universes differing in a wide range of parameters and boundary conditions. Without the assumption that such an ensemble actually exists, the explanation doesn’t get off the ground. SAP, as Leslie defines it, would be true even if there is no other universe than our own, but it would then be unable to help explain the fine-tuning. Writes Leslie:

 

It is often complained that the anthropic principle is a tautology, so can explain nothing. The answer to this is that while tautologies cannot by themselves explain anything, they can enter into explanations. The tautology that three fours make twelve can help explaining why it is risky to visit the wood when three sets of four lions entered it and only eleven exited. (Leslie 1996, pp. 170-1)

 

I would add that there is a lot more to anthropic reasoning than the anthropic principle. We discussed some of the non-trivial issues in anthropic reasoning in chapter 2, and in subsequent chapters we shall encounter even greater conundrums. Anyhow, I shall argue shortly that the above anthropic principles are too weak to do the job they are supposed to do. They are best seen as special cases of a more general principle, the Self-Sampling Assumption, which itself seems to have a methodological or epistemological status (somewhat resembling David Lewis’ Principal Principle) rather than that of a tautology pure and simple.

Anthropic hodgepodge

I have counted over thirty different "anthropic principles" in the literature. They can be divided into three categories: those that express a purported observational selection effect; those that state some speculative empirical hypothesis; and those that are too muddled or ambiguous to make any clear sense at all. The principles discussed in the previous section are in the first category. Here we will briefly review some members of the other two categories.

            Among the better-known definitions are those of physicists John Barrow and Frank Tipler, whose influential 700-pages monograph of 1986 has served to introduce anthropic reasoning to a wide audience. Their formulation of WAP is as follows:

 

(WAP_B&T) The observed values of all physical and cosmological quantities are not equally probable but they take on values restricted by the requirement that there exist sites where carbon-based life can evolve and by the requirement that the Universe be old enough for it to have already done so. (Barrow and Tipler 1986, p. 16)[14]

 

The reference to ‘carbon-based life’ does not appear in Carter’s original definition. Indeed, Carter has explicitly stated that he intended the principle to be applicable "not only by our human civilization, but also by any extraterrestrial (or non-human future-terrestrial) civilization that may exist." (Carter 1989, p. 18). It seems infelicitous to introduce a restriction to carbon-based life, and misleading to give the resulting formulation the same name as Carter’s.

            Restricting the principle to carbon-based life forms is a bad idea for another reason as well: it robs the principle of its tautological status and renders Barrow and Tipler’s position inconsistent, since they claim that WAP is a tautology. To see that WAP as defined by Barrow and Tipler is not a tautology, it is sufficient to note that it is not a tautology that all observers are carbon-based. It is no contradiction to suppose that there are observers that are implemented on some other chemical elements, and thus that there may be observed values of physical and cosmological constants that are not restricted by the requirement that carbon-based life evolves.[15]

            Realizing that the anthropic principle must not be restricted to carbon-based creatures is not a mere logical nicety. It is essential if we want to apply anthropic reasoning to hypotheses about other possible life forms that may exist or come to exist in cosmos. For example, when considering the Doomsday argument in chapter 5 this becomes crucial.

Limiting the principle to carbon-based life has the side effect of encouraging a common type of misunderstanding of what anthropic reasoning is all about. It makes it look as if it were part of a project to restore Homo sapiens to its glorious role as the Pivot of Creation. For example, Stephen Jay Gould’s 1985-criticism (Gould 1985) of the anthropic principle is based on this misconception. It is ironic that anthropic reasoning should have been attacked from this angle. Anthropic reasoning is anti-theological and anti-teleological. It holds up the prospect of an alternative explanation for the appearance of fine-tuning – the puzzlement that forms the basis for the modern version of the teleological argument for the existence of a Creator. The presence of such radical confusion is symptomatic of the primitive state of anthropic methodology, although there has been progress since Gould made his remarks.

Barrow and Tipler also provide a new formulation of SAP:

 

(SAP_B&T) The Universe must have those properties which allow life to develop within it at some stage in its history. (Barrow and Tipler 1986, p. 21)

 

On the face of it, this is rather similar to Carter’s SAP. The two definitions differ in one obvious but minor respect. Barrow and Tipler’s formulation refers to the development of life. Leslie’s version improves this to intelligent life. But Carter’s definition speaks of observers. "Observers" and "intelligent life" are not the same concept. It seems possible that there could be (and might come to be in the future) intelligent, conscious observers that are not part of what we call life – for example by lacking such properties as being self-replicating or having a metabolism etc. For reasons that will become clear later, I think that Carter’s formulation is superior in this respect. Not being alive, but being an (intelligent) observer is what matters for the purposes of anthropic reasoning.

            Barrow and Tipler have each provided their own personal formulation of SAP. Their definitions then turn out quite different:

 

Tipler: … intelligent life must evolve somewhere in any physically realistic universe. (Tipler 1982, p. 37)

 

Barrow: The Universe must contain life. (Barrow 1983, p. 149)

 

These definitions state that life must exist, which implies that life exists. The other formulations of SAP we looked at, by Carter, Barrow & Tipler, and Leslie, all stated that the universe must allow or admit the creation of life (or observers). This is most naturally read as saying only that the laws and parameters of the universe must be compatible with life – which does not imply that life exists. The propositions are clearly inequivalent.

            We are also faced with the problem of how to understand the "must". What is its modal force? Is it logical, metaphysical, epistemological or nomological? Or even theological or ethical? The definitions remain highly ambiguous until this is specified.

            Barrow and Tipler list three possible interpretations of SAP_B&T in their monograph:

 

(A)   There exists one possible Universe ‘designed’ with the goal of generating and sustaining ‘observers’.

(B)   Observers are necessary to bring the Universe into being.

(C)   An ensemble of other different universes is necessary for the existence of our Universe.

 

Since none of these are directly related to Carter’s idea about observational selection effects, I shall not discuss them further except for some brief remarks relegated to this footnote.[16]

 

A "Final Anthropic Principle" (FAP) has been defined by Tipler (Tipler 1982), Barrow (Barrow 1983) and Barrow & Tipler (Barrow and Tipler 1986) as follows:

 

Intelligent information-processing must come into existence in the universe, and, once it comes into existence, it will never die out.

 

Martin Gardner charges that FAP is more accurately named CRAP, the Completely Ridiculous Anthropic Principle. (Gardner 1986). The spirit of FAP is antithetic to Carter’s anthropic principle (Carter 1989, Leslie 1985). FAP can lay no claim to any special methodological status; it is pure speculation. The appearance to the contrary, created by affording it the honorary title of a "Principle", is presumably what prompts Gardner’s mockery.

            It may be possible to interpret FAP simply as a scientific hypothesis, and that is indeed what Barrow and Tipler set out to do. In a later book (Tipler 1994), Tipler considers the implications of FAP in more detail. He proposes what he calls the "Omega Point Theory". This theory assumes that our universe is closed, so that at some point in the future it will recollapse in a big crunch. Tipler tries to show that it is physically possible to perform an infinite number of computations during this big crunch by using the shear energy of the collapsing universe, and that the speed of a computer in the final moments can be made to diverge to infinity. Thus there could be an infinity of subjective time for beings that were running as simulations on such a computer. This idea can be empirically tested, and if present data suggesting that our universe is open are confirmed, then the Omega Point Theory will indeed have been falsified (as Tipler himself acknowledges).[17] The point I want to emphasize here is only that FAP is not in any way an application or a consequence of anthropic reasoning. (This is not to deny that anthropic reasoning may have a bearing on how evidence for speculations such as FAP should be evaluated; for example via the Doomsday argument.)

            In order to treat FAP as an empirical hypothesis, it helps if one charitably strikes out about the first part of the definition, the part which says that intelligent information processing must come into existence. I plead guilty to having done my bit to worsen inflation of anthropic principles by introducing (with my partner-in-crime, Milan C. Cirkovic) this explication – the "Final Anthropic Hypothesis" (FAH), which is the proposition that intelligent information processing will never cease (Cirkovic and Bostrom 2000). There is no particular reason to think that this proposition is true, but it may be interesting to consider what evidence there is for or against it. We find, for instance, that recent evidence for a large cosmological constant[18] (Perlmutter, Aldering et al. 1998, Reiss, Filippenko et al. 1998) only makes the situation worse for Tipler’s Omega Point Theory. There are however some other possible ways in which FAH may be true which cannot be ruled out at the present, involving poorly understood mechanisms in quantum cosmology. There are also question marks regarding which of these possible scenarios would be probabilistically acceptable in view of anthropic constraints. Studying FAH is a legitimate research objective in my view, not because there is any particular a priori or methodological reason to think that FAH is true, but because it just seems an interesting question whether intelligent observers will in fact exist for an infinitely long time in the actual world.

Inadequacy of earlier formulations

For the purposes of this dissertation, the relevant anthropic principles are those describing observational selection effects. All the formulations mentioned in this chapter’s first section are in this category. Yet, they are insufficient. They cover only a set of very special cases and fail to give an adequate expression of the idea underlying many of the most important applications of anthropic reasoning.

            One paradigmatic use of anthropic reasoning is in providing a potential explanation of fine-tuning. A satisfactory formulation of the anthropic principle should at a minimum be able to cater at least for this application. I will argue that what we’ve got so far cannot do that.

Let’s assume that the empirical precondition for the anthropic explanation of fine-tuning is satisfied, that is, that there is an ensemble of actually existing universes that differ in suitable ways with respect to their boundary conditions and physical constants. What the anthropic theorizer would then like to say is that since observers exist only in the subset of universes which are fine-tuned, the theory that there is this multiverse predicts that we should expect to observe a fine-tuned universe; and thus that the theory is supported (to some extent) by available data. Chapter 2 argued that this line of reasoning can be defended against various methodological objections. The argument still doesn’t deliver the intended conclusion, however, for it rests on the claim that intelligent life exists only in the subset of universes that are fine-tuned. But that need not be the case. In a sufficiently huge multiverse, there will also be some observers in non-tuned universes. For example, Hawking radiation from evaporating black holes is completely random in such a way that there is a finite chance that any object – such as an intelligent observer – will pop into existence outside a black hole. This finite chance is astronomically small, but never mind. If the multiverse contains a sufficient number of black holes then it is highly likely that some observers will come into existence in this manner. For such multiverses, then, one crucial premiss is false and the suggested anthropic argument consequently unsound.

 If the only relevant observational selection effect were the one expressed by SAP (much less the ones expressed by WAP or the Super-weak Anthropic Principle) then such a multiverse theory could not support an anthropic explanation of fine-tuning. It isn’t true that we couldn’t have observed a universe that weren’t fine-tuned for life – we could!

            It is not farfetched that a multiverse should be sufficiently large to make it probable that intelligent observers are generated from Hawking radiation or other random phenomena, such as thermal motion. Since thermal motion, Hawking radiation and other quantum fluctuations can occur also in non-tuned universes (ones, say, where constants don’t generally favor formation of stars or complex chemistry etc.), observers will be generated also within non-tuned universes in the multiverse. Almost all multiverse theories that have been proposed share that feature. Many multiverse theories postulate an infinite ensemble of universes. Even those that contain only a finite number might still contain sufficiently many. And even a mulitverse theory that only postulated a moderate number of different universes would still be covered by this objection, if some of the universes in it were spatially infinite, or finite but big enough. Considering that current evidence strongly suggests that our own universe is spatially infinite[19], this is a very plausible contingency.

            The SAP-explanation of the apparent fine-tuning, therefore, does not work for real multiverse theories that have been proposed. It uses the assumption that there are no observers in non-tuned universes, which is false in nearly all realistic multiverse theories.

            This may appear to be a relatively superficial objection, based on the technical point that a few freak observers will probably arise in non-tuned universes. It could be thought that this shouldn’t really matter, because it will still be true that the overwhelming majority of all observers in the multiverse will live in fine-tuned universes and will have evolved through more ordinary processes that can only take place under special conditions (fine-tuning). So if only we modify SAP slightly, to allow for a small proportion of all observers living in non-tuned universes, we could make the explanation go through.

            I suggest that this is precisely on the right line! The presence of the odd observer in a non-tuned universe changes nothing essential. And SAP should be modified or strengthened to make this clear. The idea would be that as long as the vast majority of observers are in fine-tuned universes, the ones in non-tuned universes forming a small minority, then what the multiverse theory predicts is that we should (with overwhelming probability) find ourselves in one of the fine-tuned universes. That we observe such a universe would thus be what such a multiverse theory predicts and would thus tend to confirm that theory to some degree. A multiverse theory of the right kind coupled with this ramified version of the anthropic principle could potentially account for the apparent fine-tuning of our universe.

A step in the right direction has been taken by astrophysicist Richard Gott III, who formulated the "Copernican anthropic principle":

 

[T]he location of your birth in space and time in the Universe is privileged (or special) only to the extent implied by the fact that you are an intelligent observer, that your location among intelligent observers is not special but rather picked at random from the set of all intelligent observers (past, present and future) any one of whom you could have been. (Gott 1993, p. 316)

 

This definition comes closer to giving an adequate expression of the idea behind anthropic reasoning than any of the others we have examined. It introduces an idea of randomness that can be applied to the multiverse examples under consideration: Yes, you could have lived in a non-tuned universe, but if the vast majority of observers live in fine-tuned universes then the multiverse theory predicts that you should (very probably) find yourself in a fine-tuned universe.

One problem with Gott’s definition is that it makes some problematic claims which may not be essential to anthropic reasoning. It says that your location was "picked at random". But who or what did the picking? Maybe that is too naïve a reading. Yet the expression does suggest that there is some kind of physical randomization mechanism of at work, which so to speak selects a position for you to be born at. One could imagine a possible world where this would be a good description of what was going on. Suppose God, after having created a multiverse, posts a world-map on the wall of His celestial abode, takes a few steps back and starts throwing darts at the map, creating bodies wherever they hit, and sends down souls to inhabit these bodies. Alternatively, maybe one could imagine some sort of physical apparatus, perhaps involving a time travel machine that could move about in spacetime and distribute observers in a truly random fashion. But what evidence is there that any such randomization mechanism exists? None, as far as I can see. Perhaps some subtler and less farfetched scenario could be conceived that would lead to the same result, but anthropic reasoning would be tenuous indeed had it to rely on such suppositions. As we shall see, however, that isn’t the case.

            Also, the assertion that "you could have been" any of these intelligent observers that will ever have existed is problematic. We may ultimately have to confront this problem, but it can be nice to have a definition that does not preempt that debate.

            Both these points are relatively minor quibbles. One could reasonably explicate Gott’s definition so that it comes out right in these regards. There is, however, a much more serious problem with Gott’s approach which we will discuss when examining the Doomsday argument in chapter 5. We shall therefore work with a different principle which sidesteps these difficulties.

The Self-Sampling Assumption

The preferred explication of the anthropic principle that we shall use as a starting point for the subsequent investigation is the following, which may be called the Self-Sampling Assumption:

 

(SSA) Every observer should reason as if they were a random sample drawn from the set of all observers.

 

We will elaborate as we go along on what this means and how it is indented to be used, but some clarifications can be made right away. I use "observer" here as a technical term for whatever sort of entity is such that one should reason as if one were randomly selected from the class of all those entities. What this class is, is a topic for later discussions. It is intended to include at least you and me and other beings that are "like us" in relevant ways. We shall call the class of all observers that will ever have existed the "reference class". (We will revise this terminology in chapter 9, where we introduce an important modification to SSA and allow reference classes that consists of only a subset of all observers. The motivation for those changes will become understandable only after we have thoroughly investigated the implications of SSA as formulated above. So meanwhile we can think of the reference class as the class of all observers and observers as those entities from which to reason as if you were a random sample.)

            The above statement of SSA is vague in at least two important respects: What counts as an observer? And what is the sampling density with which you have been sampled? The resolution of these areas of vagueness matters a lot for what empirical predictions you get from applying SSA in concrete applications. However, while it is important to examine these issues (which we shall do in later chapters), many interesting philosophical problems in anthropic reasoning do not hinge on them. We can sidestep the potentially problematic areas of vagueness by making the following simplifying assumptions:

            Consider an imaginary world where we have no borderline cases of what counts as an observer and where the observers are sufficiently similar to each other to justify using a uniform sampling density (rather then one, say, where long-lived observers get a proportionately greater weight). Thus let’s suppose (merely for the sake of illustration) that the only observers are human beings on the planet Earth, that we have no evolutionary ancestors, that all humans are fully self-aware and are knowledgeable about probability theory and anthropic reasoning, etc., that we all have identical life spans and that we are equal in any other arguably relevant respect. Assume furthermore that each human has a unique birth rank, denoting her temporal position in the human species[20], and that the total number of humans that will ever have lived is finite.

            Under these assumptions, we get as a Corollary from the SSA that

 

(D)       ,

 

where R and N are random variables: N representing the total number of people that will have lived, and R the birth rank of the particular person doing the reasoning. I call this expression "D" because, as we shall see later, it is used in the derivation of the Doomsday argument.

            The other observational selection principles discussed above are special cases of SSA. Take first WAP (in Carter and Leslie’s rendition). If a theory T says that there is only one universe and some regions of it contain no observers, then WAP says that T predicts that we don’t observe one of those observerless regions. (That is, that we don’t observe them "from the inside". If the region is observable from a region where there are observers, then obviously it could be observable by those observers.) SSA yields the same result, since if there is no observer in a region, then there is zero probability that a sample taken from the set of all observers will be in that region, and hence zero probability that you should observe that region given the truth of T.

            Similarly, if T says there are multiple universes, only some of which contains observers, then SAP (again in Carter and Leslie’s sense) says that T predicts that what you should observe is one of the universes that contain observers. SSA says the same, since it assigns zero sampling density to being an observer in an observerless universe.

            In the next chapter we shall consider ways of generalizing D. SSA and its corollaries are to be understood as methodological prescriptions, stating how probabilistic inferences are to be made in certain cases.[21] We will provide several arguments for adopting SSA. However, it is not a major concern for our purposes whether SSA is strictly a "requirement of rationality". It suffices if many intelligent people do in fact – on reflection – have a subjective prior probability function that satisfies SSA. If that is acknowledged, it follows that investigating surprising consequences for important matters that flow from SSA will be worth the effort.

CHAPTER 4: WHY ACCEPT THE SELF-SAMPLING ASSUMPTION?

This chapter gives reasons for accepting SSA. In the process of so doing, it also illustrates some aspects of the principle’s intended meaning and begins to develop a theory of how SSA can be used in concrete scientific contexts.

            The case for accepting SSA can be divided into two parts. One part focuses on the application. I will argue that some methodological rule is needed to derive observational consequences in cosmology; that other candidate rules that have been proposed are inadequate; and that SSA provides the services we require. SSA also gives methodological guidance for some types of inferences in other fields, including thermodynamics, evolutionary biology, and traffic planning. The other part presents a series of thought experiments designed to demonstrate that it is reasonable to reason in accordance with SSA in a wide range of circumstance. If the application-part can be likened to field observations, the thought experiments are more like laboratory research where we have full control over all relevant variables and can stipulate away inessential complications and hopefully get a finer measurement of our intuitions and epistemic convictions regarding SSA. We begin by presenting this latter part of the case for SSA, returning to the application-based argument towards the end of this chapter.

Prison

Our first gedanken is Prison:

 

Imagine a world that consists of a prison with one hundred cells. In each cell there is one person. Ninety of the cells are painted blue on the outside and the other ten are painted red. Each person is asked to guess whether she is in a blue or a red cell. (And everybody knows all this.) Suppose you find yourself in one of these cells. What color should you think it has? – Answer: You should think that with 90% probability it is blue.

 

            Since 90% of all people are in blue cells, and as you don’t have any other relevant information, it seems you should think, in agreement with SSA, that with 90% probability you are in a blue cell. Most people the author has talked to agree that this is the intuitively correct answer. Since the example does not depend on the particular numbers involved, we thus have a large class of cases where SSA provides plausible guidance for what to believe.[22] Some of our subsequent investigations in this chapter will consider arguments for extending this class in various ways. It may nonetheless be worthwhile reflecting on whether it is possible to push the argument further to try to convince a hypothetical skeptic who isn’t immediately persuaded to set her credence equal to 90% in Prison.

            Consider the following argument. Suppose everyone accepts SSA and everyone has to bet on whether they are in a blue or a red cell. Then 90% of all prisoners will win their bets and 10% will lose. Suppose, on the other hand, that SSA is rejected and people think that one is no more likely to be in a blue cell; so they bet by flipping a coin. Then, on average, 50% of the persons will win and 50% will lose. It seems better that SSA be accepted.

            This argument is incomplete as it stands. Just because one pattern A of betting leads more people to win their bets than another pattern B, we shouldn’t think that it is rational for anybody to bet in accordance with pattern A rather than B. In Prison, consider the betting pattern A which specifies that "If you are Harry Smith, bet you are in a red cell; if you are Helena Singh, bet that you are in a blue cell; …" – such that for each person in the experiment, A gives the advice that will lead him or her to be right. Adopting rule A will lead to more people winning their bets (100%) than any other rule. In particular, it outperforms SSA which has a mere 90% success rate.

            Intuitively it is clear that rules like A are cheating. This is maybe best seen if we put A in the context of its rival permutations A’, A’’, A’’’ etc., which map the captives’ names to recommendations about betting red or blue in other ways than does A. Most of these permutations do rather badly. On average they give no better advice than would flipping a coin, which we saw was inferior to accepting SSA. Only if the people in the cells could pick the right A-permutation would they benefit. In Prison they don’t have any information enabling them to do this. If they picked A and consequently benefited, it would be pure luck.

            What allows the people in Prison to do better than chance is that they have a relevant piece of empirical information regarding the distribution of observers over the two types of cells. They have been informed that 90% of them are in blue cells, and it would be irrational of them not to take this information into account. We can imagine a series of thought experiments where an increasingly large fraction of observers are in blue cells – 91%, 92%, …, 99%. The situation gradually degenerates into the 100%-case where they are told, "You are all in blue cells.", from which each can deductively infer that she is in a blue cell. As the situation approaches this limiting case, it is plausible to require that the strength of participants’ beliefs about being in a blue cell should gradually approach probability 1. SSA has this property.

            One may notice that while it is true if the detainees adopt SSA then 90% of them win their bets, yet there are even simpler methods that produce the same result. For instance: "Set your probability of being in a blue cell equal to 1 if most people are in blue cells; and to 0 otherwise." Using this epistemic rule will also result in 90% of the people winning their bets. Such a rule would not be attractive however. First, when the participants step out of their cells, some of them will find that they were in red cells. Yet if their prior probability of that were zero, they could never learn that by Bayesian belief updating. The second and more generic point is that when we consider rational betting quotients, rules like this are revealed to be inferior. A person whose probability for finding herself in a blue cell was 1 would be willing to bet on that hypothesis at any odds[23]. The people following this simplified rule would thus risk losing arbitrarily great sums of money for an arbitrarily small and uncertain gain – an uninviting strategy. Moreover, collectively, they would be guaranteed to lose an arbitrarily large sum.

            Suppose we agree that all the participants should assign the same probability to being in a blue cell (which is quite plausible since their evidence does not differ in any relevant way). It is then easy to show that out of all possible probabilities they could assign to finding themselves in blue cells, a probability of 90% is the only one which would make it impossible to bet against them in such a way that they were collectively guaranteed to lose money. And in general, if we vary the numbers of the example, their degree of belief would in each case have to be what SSA prescribes in order to save them from being a collective sucker.

            On an individual level, if we imagine the experiment repeated many times, the only way a given participant could avoid having a negative expected outcome when betting repeatedly against a shrewd outsider would be by setting her odds in accordance with SSA.

            All these considerations support what seems to be most persons’ initial intuition about Prison: that it is a situation where one should reason in accordance with SSA. Any plausible principle of the epistemology of information with an indexical component would have to agree with SSA’s verdicts in this particular case.

            One important thing to notice in Prison is that it was not specified how the hundred inmates came to be in the cells they are in. That doesn’t matter so long as the inmates don’t know anything about it which gives them evidence about what color cell they are in. Thus, they may have been allocated to their respective cells through some objectively random mechanism such as drawing tickets from a lottery urn, then being blindfolded and led to their designated locations. Or they may have been allowed to choose cells for themselves, and a random mechanism subsequently activated to determine which cells should be painted. But the thought experiment does not depend on there being a well-defined randomization mechanism. One may just as well imagine that prisoners have been in their cells since their birth, or since the beginning of the universe. If there is a possible world where the laws of nature directly specify which individuals are to appear in which cells, without any appeal to initial conditions, the persons in the experiment would still be rational to follow SSA provided that they did not have knowledge of the laws or were incapable of deducing what the laws implied about their own situation. Objective chance, therefore, is not a necessary ingredient in the gedanken. The fuel is subjective uncertainty.

Emeralds

We shall now look at an argument for extending the range of cases where SSA can be applied. We shall see that the synchronous nature of Prison is an inessential feature: you can in some contexts legitimately reason as if you were a random sample from a reference class that includes observers that exist at different times. Also, we will find that one and the same reference class can contain observers that differ in many respects, including their genes and gender. To this effect, consider an example due to John Leslie:

 

Imagine an experiment planned as follows. At some point in time, three humans would each be given an emerald. Several centuries afterwards, when a completely different set of humans was alive, five thousand humans would each be given an emerald. Imagine next that you have yourself been given an emerald in the experiment. You have no knowledge, however, of whether your century is the earlier century in which just three people were to be in this situation, or in the later century in which five thousand were to be in it. ...

Suppose you in fact betted that you lived [in the earlier century]. If every emerald-getter in the experiment betted in this way, there would be five thousand losers and only three winners. The sensible bet, therefore, is that yours is instead the later century of the two. (Leslie 1996, p. 20)

 

For reasons which need not concern us here (but will be discussed in a later chapter), it is convenient to focus on a slightly modified version of Leslie’s example, one where the two batches of people are the only observers ever to exist. One could invent a fairy tale about how the intervening generations had their brains sucked out and replaced with clever clockworks by an evil mollusk, but we skip the fluff.

            The same arguments that were made for SSA in Prison can be made for SSA in Emeralds. Leslie makes the point about more people being right if everyone bets that they are in the later of the two centuries. As we saw in the previous section, this point needs to be supplemented by additional arguments before it yields support for SSA. (Leslie gives the emeralds example as a response to one objection against the Doomsday argument. He never formulates SSA, but parts of his arguments in defense of the Doomsday argument and parts of his account of anthropic reasoning in cosmology are directly relevant to evaluating SSA.)

Two Batches

As Leslie notes, we can learn a second lesson if we consider a variant of the emeralds example:

 

A firm plan was formed to rear humans in two batches: the first batch to be of three humans of one sex, the second of five thousand of the other sex. The plan called for rearing the first batch in one century. Many centuries later, the five thousand humans of the other sex would be reared. Imagine that you learn you’re one of the humans in question. You don’t know which centuries the plan specified, but you are aware of being female. You very reasonably conclude that the large batch was to be female, almost certainly. If adopted by every human in the experiment, the policy of betting that the large batch was of the same sex as oneself would yield only three failures and five thousand successes. ... [Y]ou mustn’t say: ‘My genes are female, so I have to observe myself to be female, no matter whether the female batch was to be small or large. Hence I can have no special reason for believing it was to be large.’ (pp. 222-3)

 

If we accept this, we can conclude that members of both genders can be in the same reference class. In a similar fashion, one can argue for the irrelevance of short or tall, black or white, rich or poor, famous or obscure, fierce or meek etc. If analogous arguments with two batches of people with any of those property pairs are accepted, then we have quite a broad reference class already. We shall return in a moment to consider what limits there might be to how wide the reference class can be, but first we want to look at another dimension in which one may seek to extend the applicability of SSA.

God’s Coin Toss

All the examples so far have been of situations where all the competing hypotheses entail the same number of observers in existence. A very important new element is introduced in cases where the total number of observers is different depending on which hypothesis is true. Here is a simple gedanken where this happens.

 

God’s Coin Toss, version one (G1). God[24] starts by tossing a fair coin. If the coin falls tails then He creates one room and a man with a black beard inside it. If the coin falls heads then He creates two rooms, one with a man with a black beard and one with a man with a red beard. Apart from this, the world is empty, and everyone knows all the above. You find yourself in a room and you know that you have black beard. Question: What should be your credence that the coin fell heads?

 

Consider the following three models of what probability you should rationally assign to the proposition that the coin fell heads:

 

Model 1 (Naïve). There are two possibilities, Heads or Tails; the coin is known to be fair; both possibilities are perfectly compatible with what you know.

P(Heads) = P(¬Heads) = 1/2.

Therefore, your credence of Heads should be 1/2.

 

Model 2 (SSA). If you had had red beard, you could have inferred that there were two rooms, which entails Heads. Knowing that you have black beard does not allow you to rule out either possibility but it is still relevant information. This can be seen by the following argument. The prior probability of Heads is one half, since the coin was fair. If the coin fell Heads then the only observer in existence has a black beard; hence by SSA the conditional probability of having a black beard given Heads is one. If the coin fell Tails then one out of two observers has a black beard; hence, also by SSA, the conditional probability of black beard given Tails is one half. That is, we have

P(Heads) = P(¬Heads) = 1/2

P(Black | Heads) = 1/2

P(Black | ¬Heads) = 1

By Bayes’ theorem, the posterior probability of Heads, after conditionalizing on Black, is

P(Heads | Black)

= 1/3.

Therefore, your credence of Heads should be 1/3.

 

Model 3 (SSA&SIA). It is twice as likely that you should exist if two observers exist than if only one observer exists. This follows if we make the Self-Indication Assumption (SIA), to be explained shortly. The prior probability of Heads should therefore be 2/3, and of Tails 1/3. As in Model 2, the conditional probability of black beard given Heads is 1 and the conditional probability of black beard given Tails is 1/2.

P(Heads) = 2/3

P(¬Heads) = 1/3

P(Black | Heads) = 1/2

P(Black | ¬Heads) = 1

By Bayes’ theorem, we get

= 1/2.

Therefore, your credence of Heads should be 1/2.

 

The last model uses something that we can dub the Self-Indication Assumption, according to which you should conclude from the fact that you came into existence that probably quite a few observers did:

 

(SIA) Given the fact that you exist, you should (other things equal) favor hypotheses according to which many observers exist over hypotheses on which few observers exist.

 

SIA may seem prima facie implausible, and I shall argue in chapter 6 that it is no less implausible ultimo facie. Yet some of the more profound criticisms of specific anthropic inferences rely implicitly on SIA. In particular, adopting SIA annihilates the Doomsday argument. It is therefore good to put it on the table so we can consider what reasons there are for accepting or rejecting it. To give SIA the best chance it can get, we postpone this evaluation until we have discussed the Doomsday argument and have seen why a range of more straightforward objections against the Doomsday argument fail. The fact that SIA could seem to be the only coherent way of resisting the Doomsday argument is possibly the strongest argument that can be made in its favor.

            For the time being, we put SIA to one side (i.e. we assume that it is false) and focus on comparing Model 1 and Model 2. The difference between these models is that Model 2 uses SSA and Model 1 doesn’t. By determining which of these models is correct, we get a test of whether SSA should be applied in epistemic situations where hypotheses implying different numbers of observers are entertained. If we find that Model 2 (or, for that matter, Model 3) is correct, we have extended the applicability of SSA beyond what was established in the previous sections, where the number of observers did not vary between the hypotheses under consideration.

            In Model 1 we are told to consider the objective chance of 50% of the coin falling heads. Since you know about this chance, you should according to Model 1 set your subjective credence equal to it.

            The step from knowing about the objective chance to setting your credence equal to it follows from the so-called Principal Principle[25]. This is not the place to delve into the details of the debates surrounding this principle and the connection between chance and credence (Bigelow, Collins et al. 1993, Sturgeon 1998, Black 1998, Bostrom 1999, Hall 1994, Hoefer 1997, Hoefer 1999, Vranas 1998, Thau 1994, Strevens 1995, Halpin 1994, Kyburg(Jr.) 1981, Skyrms 1980). Suffice it to point out that the Principal Principle does not say that you should always set your credence equal to the corresponding objective chance if you know it. Instead, it says that you should do this unless you have other relevant information that should be taken into account. There is some controversy about how to specify what types of such additional information will modify reasonable credence when the objective chance is known, and what types of additional information leave the identity intact. But there is general agreement that the proviso is needed. For example, no matter how objectively chancy a process is, and no matter how well you know the chance, if you have actually seen what the outcome was then your credence in that observed outcome should of course be one (or extremely close to one) and your credence in any other outcome the process could have had should be (very close to) zero; and this is so quite independently of what the objective chance was. None of this is controversial.

            Now the point is that in God’s Coin Toss you have such extra relevant information that you need to take into account, and Model 1 fails to do that. The extra information is that you have black beard. This information is relevant because it bears probabilistically on whether the coin fell heads or tails. We can see this as follows. Suppose you are in a room but you don’t know what color your beard is. You are just about to look in the mirror. If the information that you have black beard weren’t probabilistically relevant to how the coin fell, then there would be no need for you to change your credence about the outcome after looking in the mirror. But this is an incoherent position. For there are two things you may find when looking in the mirror: that you have black beard or that you have red beard. Before you peek in the mirror, you know that if you find that you have red beard then you will have conclusively refuted the hypothesis that the coin fell tails. So the mirror might give you information that would increase your credence of Heads (to 1). But that entails that making the other possible finding (that you have black beard) must decrease your credence in Heads. In other words, your conditional credence of Heads given Black beard must be less than your unconditional credence of Heads.

            If your conditional probability of Heads given black beard were not lower than the probability you assign to Heads, while also your conditional probability of Heads given red beard is one, then you would be incoherent. This is easily shown by a standard Dutch book argument, or more simply by the following little calculation:

 

Write h for the hypothesis that the coin fell heads, and e for the evidence that you have black beard. We can assume that . Then we have

and

.

Dividing these two equations and using , we get

.

So the quotients between the probabilities of h and ¬h is less after e is known than before. In other words, learning e decreases the probability of h and increases the probability of ¬h.

 

So the observation that you have black beard gives you relevant information that you need to take into account and it should lower your credence of Tails to below your unconditional credence of Tails, which (provided we reject SIA) is 50%. Model 1, which fails to do this, is therefore wrong.

            Model 2 does take the information about your beard color into account and sets your posterior credence of Heads to 1/3, lower than it would have been had you not seen your beard. This is a consequence of SSA. The exact figure depends on the assumption that your conditional probability of Black beard equals that of Red beard, given Heads. If you knew that the coin landed heads but you hadn’t yet looked in the mirror, you would know that there was one man with red beard and one with black, and provided these men were sufficiently similar in other respects (so that from your present position of ignorance about your beard color you didn’t have any evidence as to which one of them you are) these conditional credences should both be 50% according to SSA.

            If we agree that Model 2 is the correct one for God’s Coin Toss then we have seen how SSA can be applied to problems where the total number of observers in existence is not known. In chapter 9, we will reexamine God’s Coin Toss and argue for adoption of a fourth model, which conflicts with Model 2 in subtle but important ways. The motivation for doing this, however, will become clear only after detailed investigations into the consequences of accepting Model 2. So for the time being, we will adopt Model 2 as our working assumption in order to explore the implications of the way of thinking it embodies.

If we combine this with the lessons of the previous gedanken, we now have a very wide class of problems where SSA can be applied. In particular, we can apply it to reference classes that contain observers that live at different times; that are different in many substantial ways including genes and gender; and that may be of different sizes depending on which hypothesis under consideration is true.

One may wonder if there are any limits at all to how much we can include in the reference class. There are. We shall now see why.

The reference class problem

The reference class, remember, was preliminarily defined to consist of all observers that will ever have existed. But what, precisely, counts as an observer? "Observer" was introduced as a technical term and its exact meaning has yet to be determined. We have seen examples of things that must be included in the reference class. In order to complete the definition, we also have to specify what things must be excluded. The problem of the reference class is to define what counts as an observer for the purposes of SSA.

In many cases where the total number of observers is the same on any of the hypotheses assigned non-zero probability, the problem of the reference class does not seem to be relevant. For instance, take Prison and suppose that in ten of the blue cells there is a polar bear instead of a human observer. Now, whether the polar bears count as observers makes no difference. Whether they do or not, you know you are not one of them. And you thus know that you are not in one of the ten cells they occupy. You therefore recalculate the probability of being in a blue cell to be 80/90, since 80 out of the 90 observers that you – for all you know – might be, are in blue cells. Here you have simply eliminated the ten ice-bear cells from the calculation. But this does not rely on the assumption that polar bears don’t count as observers. The calculation would come out exactly the same if the bears were replaced with human observers who were very much like yourself, provided you knew you were not one of them. Maybe you are told that ten people who have a birthmark on their right calves are in blue cells. After verifying that you yourself don’t have such a birthmark, you adjust your probability of being in a blue cell to 80/90. This is in agreement with SSA. According to SSA, Pr(Blue cell | Setup) = 90/100. But also by SSA, Pr(Blue cell | Setup & Ten of the people in blue cells have birth marks of a type you don’t have) = 80/90.

            One place where the reference class problem becomes crucial is where the total number of observers is unknown. Consider the following variant of God’s Coin Toss. There are two rooms. Whatever way the coin falls, a person with a black beard is created in room one. If and only if it falls heads, then one other thing x is created in room two. You find yourself in one of the rooms and you are informed that it is room number one. We can now ask, for various choices of x, what your credence should be that the coin fell heads.

            The original version (G1) was one where x is a man with red beard:

 

 

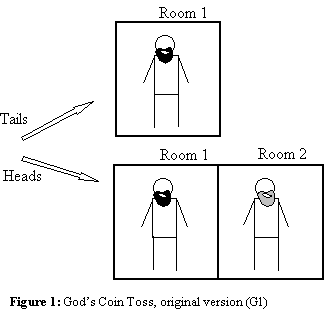
As we saw above, on Model 2 ("SSA and not SIA"), your credence of Heads in this case is 1/3. But now consider a second case (G2) where we let x be a stone:

 

 

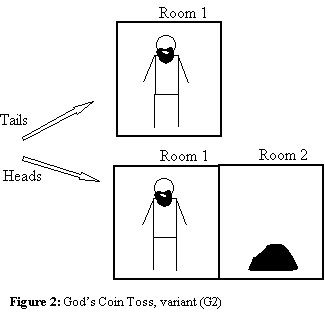
In G2, when you find that you are the man in room one, it seems clear that your credence of heads should be 1/2. The conditional probability of you observing what you are observing (i.e. your being the man in room one) is 1 on both Heads and Tails in this case, because you couldn’t possibly have found yourself observing being in room two. (We are assuming that the stone does not have a soul or a mind of course.) Notice that the arguments used to argue for SSA in the previous examples cannot be used in G2. A stone cannot bet, or be wrong, so the fraction of observers who are right or would win their bets here is not improved by adopting SSA. Moreover, it seems impossible to conceive of a situation where you would be ignorant as to whether you were the man in room one or the stone in room two.

            If this is right then the probability you should assign to Heads depends on what you know would be in room two if the coin fell heads, even though you know that you are in room one. The reference class problem can be relevant in cases like this, where the total number of observers vary depending on which hypothesis is true, because what you should believe depends on whether the object x that would be in room two would be in the reference class or not. It makes a difference to your rational credence whether x is stone or an observer like yourself.

            Stones, consequently, are not in the reference class. In a similar vein we can rule out tables, planets, books, plants, bacteria and other such non-observer entities. It gets trickier when we consider possible borderline cases such as a gifted chimpanzee, a Neanderthal or a mentally handicapped human. It is not immediately obvious whether the earlier arguments for including things in the reference class could be used to argue that these entities should be allowed in. Can a severely mentally handicapped person bet? Could you have found yourself as such a person? (Although anybody could of course in one sense become severely mentally disabled, it could be argued that the being that results from such a process would not in any real sense still be "you" if the damage is sufficiently severe.)[26]

            Intellectual insufficiency is not the only prima facie source of vagueness or indeterminacy of the reference class. Here is a list of possible borderlines:

 

·        Insufficient intellectual abilities (e.g. chimpanzees; mentally handicapped persons; Neanderthals; persons who can’t understand SSA and the probabilistic reasoning involved in using it in the application in question)

·        Insufficient information (e.g. persons who don’t know about the experimental setup)

·        Lack of some occurrent thoughts (e.g. persons who, as it happens, don’t think of applying SSA to the situation in question, although they have the capacity to do so)

·        Exotic mentality (e.g. angels; superintelligent computers; posthumans)

 

I don’t want to make any claim as to whether the reference class should be delimited in such a way that vagueness can arise in all of these four zones. For instance, maybe it is not possible to disqualify an intellect for being too intelligent. I only want to note that the exact way of delimiting the reference class has not yet been settled, and in order to do so one would have to address these four points. We will return to the reference class problem in the next chapter, where I will show that an attempted solution by John Leslie fails.

The sampling density

Closely related to the reference class problem is the problem of selecting the sampling density that you should reason as if you had been sampled with from the reference class. (The reference class problem can be seen as a special case of this: the problem of which objects should be assigned zero sampling density.) We have seen examples where all observers are similar in all respects that could plausibly be thought to make a difference to their sampling density and where consequently a uniform sampling density over all the objects in the reference class is justified, in accordance with expression D (chapter 3). In most real-world applications, however, observers differ in many respects, including ones which may be thought relevant to their sampling density.

            To begin with, we can consider some easy cases which are covered by what has already been said. Modify God’s Coin Toss so that now there are two observers in room one (independently of how the coin fell):

 

 

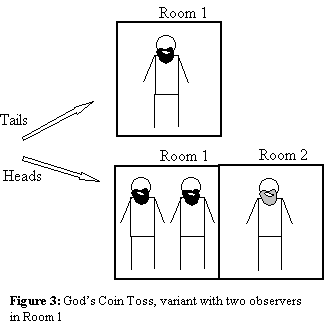
This changes the odds as follows:

P(Heads) = P(¬Heads) = 1/2

P(Black | Heads) = 2/3

P(Black | ¬Heads) = 1,

which gives

P(Heads | Black) = 2/5.

 

The result is of course the same if the two persons in room one are Siamese twins and share the same body. As long as it is only a matter of the number of observers changing, the case will be covered by the preceding discussion. But what happens if we keep the number of observers constant while varying their nature? Can different choices of x (the potential content of room two) lead to different values of the credence you should assign to Heads, even when x ranges only over different types of observers?

            We can take a first step towards specifying the sampling density by substituting "observer-moments" for "observers". Different observers may live differently long lives, be awake different amounts of time, spend different amounts of time engaging in anthropic reasoning etc. If we chop up the stretch of time an observer exists into discrete observer-moments then we have a natural way of weighing in these differences. We can redefine the reference class to consist of all observer-moments that will ever have existed. That is, we can upgrade SSA to something we can call the Strong Self-Sampling Assumption:

 

(SSSA) Every observer at every moment should reason as if their present observer-moment were randomly sampled from the set of all observer-moments.

 

Just as we previously could assume a uniform sampling density over the set of all observers in case they were identical in every relevant respect, as expressed by D, we can now formulate a stronger version of D by adding that the sampling density should be uniform over all observer-moments provided they are identical in all relevant respects:

 

(SD)     ,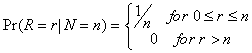

 

where N now represents the total number of observer-moments and R the rank of your present observer-moment.

            SSSA is a strengthening of SSA (and SD is a strengthening of D). In the special case where all observers in existence each consists of the same number of observer-moments, SSSA (and SD) can be derived from SSA (and D). But in the more general case where the number of observer-moments is not equal for all observers then SSSA may yield a definite sampling density (provided only that the observer-moments are relevantly similar) where SSA would not (since the observers are not relevantly similar).

            It could be thought that there is some arbitrariness as to how long a period of an observer we count as an observer-moment. So long as the observer-moments are short compared to the typical duration of an observer, however, that does not matter provided we partition all observers into segments of equal length. To illustrate this point, consider the following gedanken:

 

 

Only one observer exists. This observer is first in room one where he stays for two hours. Then he is given a drug that induces retrograde amnesia (causing him to forget that he has been in room one), and he is transported into room two where he spends one hour, whereupon he is terminated. (In each room he is informed about the general setup of the experiment, so he always knows that.)

 

If we adopt SSSA then at each point in time this observer should believe with probability 2/3 that he is currently in Room 1 and with probability 1/3 that he is currently in Room 2. This is so because he knows that two thirds of all observer-moments are in Room 1 and only one third in Room 2, and he does not have any means of determining which of these observer-moments is his present one. And it is easy to see that this holds whether we stipulate that an observer-moment is one second or five minutes long.

            The calculation is exactly the same if instead of one observer being transported from one room to the other we have two different observers that each exist in one of the rooms for two hours and one hour, respectively:

 

 

In this case too, by the same reasoning, both observers should at each time set: [27]

P(I am currently in Room 1) = 2/3, and

P(I am currently in Room 2) = 1/3.

 

Cases where the total number of observer-moments may differ depending on which hypothesis is true (such as in a temporal version of God’s Coin Toss) are handled in similar manner as before – just replace "observer" with "observer-moments".

            When using SSSA, it may be appropriate to segment observers into segments of equal subjective time. If one observer thinks twice as many thoughts and has twice the number of experiences in a given time interval as another observer, it seems quite plausible to associate twice as many observer-moments to the former observer as to the latter observer during the interval. Thus, for instance, if two similar observers are implemented on two distinct pieces of silicon hardware, and we run one of the computers at a faster clock rate, then on this line of reasoning that should result in more observer-moments being produced per second in the faster computer.

            The fact that subjective time seems the appropriate measure of the duration of observer-moments may indicate that the still more fundamental entity in the reference class should be (some types of) thoughts, or occurrent ideas. Just as longer-lived observers get a higher sampling density by virtue of containing more observer-moments, so should perhaps also observer-periods of equal objective duration get a higher sampling density by virtue of containing a greater number of occurrent thoughts.[28]

            We shall leave this discussion without having tied up all the ends.[29] The various strengthening of SSA will not be assumed in what follows, except in the traffic planning example later in this chapter and in chapter 9 where we will discuss some ideas that presuppose SSSA. These are intriguing issues however, which may be further explored to develop a more complete theory of how to reason in epistemic situations involving observational selection effects or indexical uncertainty. Developing such a more complete theory is important for three reasons. First, it may potentially increase the range of practical applications. Second, it may affect radically the results in some applications, e.g. where we use SSA on a reference class of observers that are not quite equal in all relevant ways. And third, it would boost our confidence in the methodological soundness of anthropic reasoning if we had a neat and plausible solution to the problem of the reference class. (Conversely, it would somewhat undermine our confidence if it turned out that there were no such solution but instead a vast wasteland of indeterminacy and arbitrariness.)

SSA in cosmology

We now turn to consider the application-based arguments for SSA. I shall argue that SSA codifies and legitimates certain plausible epistemological practices and that there are elements in scientific methodology which seem rely on an implicit appeal to SSA.

            Let’s begin with cosmology. We need a rule for how to derive observational consequences from the multiverse theories. Such theories are popular in contemporary cosmology. But without some idea of what such a theory predicts that we should observe, we would have no way of testing it empirically. It would be scientifically unfruitful to construe multiverse theories in a manner such that they yielded no observational implications. It would go against scientific practice; for cosmologists discussing multiverse theories are constantly evaluating those theories in light of new data, occasionally modifying them accordingly. So there is some connection to observation. The question is, what is this connection and how can it be analyzed? I shall assume that the connection is probabilistic in nature, for astronomic evidence typically counts more or less strongly in favor or against some multiverse theory but does not usually falsify or refute it conclusively. What is needed is thus some methodological principle or account of how probabilistic observational consequences are to be derived from a multiverse theory.

            One such principle that has been proposed is SAP (which we take here in Leslie’s sense). A multiverse theory combined with SAP yields observational consequences in some cases. SAP has gained quite widespread implicit or explicit acceptance among those trying to frame anthropic explanations for the apparent fine-tuning of our universe. However, I argued in chapter 3 that SAP is inadequate and gives an incorrect account of anthropic reasoning. In particular, SAP fails to take into account that different universes may contain vastly different numbers of observers and that a multiverse theory should not be thought to imply that we should probably observe that we are, say, black hole phenomena, at least not if the theory implies that the vast majority of all observers do not observe that they are black hole phenomena (even if the majority of universes only have observers that do observe that). SAP therefore does not supply the methodological rule we are looking for.

            Instead we formulated another principle, SSA, and suggested that it provides a more plausible account of anthropic reasoning. SSA gives what seems like the right result in the freak-observers-from-black-holes example, namely that if such a multiverse theory is true then we should not expect to be black hole phenomena although there is some astronomically tiny probability that we would observe that. More generally: If, according to some multiverse theory T, almost all observers are in one particular type K of universe, then according to SSA, T predicts that we probably observe a type-K universe. Observing that we are not in a type-K universe would be evidence against T, whilst observing that we are in a type-K universe would tend to confirm T at least slightly – how much depends on what probability plausible rival theories to T assign to us being in a type-K universe.

            SSA also works to our advantage in single-universe cosmologies. If we live in a sufficiently large universe then there are lots of freak observers from black holes in our universe. But this obviously does not entail that it is anything other than extremely unlikely that we are such observers, because only a tiny minority[30] of all observers are freak observers. WAP (in Carter and Leslie’s sense) says only that a theory should be taken to assign zero probability to us making observations which would only be made by observers existing in regions where according to the theory there are no observers. But that is not enough to explain why we shouldn’t expect to be freak observers. We need the stronger principle SSA to be able to derive that result.

SSA in thermodynamics, and time’s arrow

In this section we examine Boltzmann’s famous proposal for how to explain why entropy is increasing in the forward time-direction. I will show that a popular objection against Boltzmann relies on an implicit appeal to SSA. Since this objection is intuitively plausible, when it is discovered that SSA is required to underwrite it one can take this to give some reason for accepting SSA.

            The outlines of Boltzmann’s[31] attempted explanation can be sketched roughly as follows. The direction of time’s arrow appears to be connected to the fact that entropy increases in the forward time-direction. Now, if one assumes, as is commonly done, that low entropy corresponds in some sense to low probability, then one can see that if a system starts out in a low-entropy state then it will probably evolve over time into a higher entropy state, which after all is a more probable state of the system. The problem of explaining why entropy is increasing is thus reduced to the problem of explaining why entropy is currently so low. This would appear to be a priori improbable. However, Boltzmann points out that in a sufficiently large system – and the universe may be such a system if it extends very far beyond the range of current telescopes, as it may well do – there are (with high probability) local regions of the system, let’s call them "subsystems", which are in low-entropy states even if the system as a whole is in high-entropy state. (Think of it like this: in a sufficiently large container of gas, there will be some places where all the gas molecules in that local region are lumped together in a small cube or some other neat pattern. That is probabilistically guaranteed by the random motion of the gas molecules in the container and the fact that there are so many of them.) Thus, Boltzmann argued, in a large enough universe, there will be some regions and some times when just by chance the entropy in those regions happens to be exceptionally low. Since life can only exist in a region if it has very low entropy, we would naturally find that in our part of the universe entropy is very low. Since low-entropy subsystems are very likely to move towards higher-entropy states, we thus have an explanation of why entropy is currently low and increasing. An observational selection effect guarantees that we observe a region where that is the case, even if such regions are enormously sparse in the bigger picture.

            Lawrence Sklar remarks of Boltzmann’s explanation that it has been "credited by many as one of the most ingenious proposals in the history of science, and disparaged by others as the last, patently desperate, ad hoc attempt to save an obviously failed theory" (Sklar 1993, p. 44). My feeling is that the ingenuity of the Boltzmann’s contribution should be granted, especially considering that writing this in 1895 he was nearly seventy years ahead of his time in directly considering observational selection effects when reasoning about the large-scale structure of the world. Nonetheless, the idea is flawed.

            The standard objection is that Boltzmann’s datum – that the observable universe is a low-entropy subsystem –turns out on a closer look to be in conflict with his explanation. It is noted that very large low-entropy regions, such as the one we observe, are very sparsely distributed if the universe as a whole is in a high-entropy state. A much smaller low-entropy region would have sufficed to permit intelligent life to exist. Boltzmann's theory fails to account for why the observed low-entropy region is so large and so grossly out of equilibrium.

This reasonable objection can be fleshed out in terms of SSA. Let us follow Boltzmann and suppose that we are living in a very vast (perhaps infinite) universe which is in thermal equilibrium and that observers can exist only in low-entropy regions. Let T be the theory that asserts this. According to SSA, what T predicts we should observe depends on where T says that the bulk of observers tend to be. Since T is a theory of thermodynamic fluctuations, it implies that smaller fluctuations (i.e. low-entropy regions) are vastly more frequent than larger fluctuations, and hence that most observers will find themselves in rather small fluctuations. This is so because the infrequency of larger fluctuations increases rapidly enough to make sure that even though a given large fluctuation will typically contain more observers than a given small fluctuation, the previous sentence nonetheless holds true. By SSA, T assigns a probability to us observing what we actually observe that is proportional to the fraction of all observers it says would make that kind of observations. Since an extremely small fraction of all observers will observe a low entropy region as large as ours if T is true, it follows that T gives an extremely small probability to the hypothesis that we should observe such a large low-entropy region. Hence T is heavily disfavored by our empirical evidence and should be rejected unless its a priori probability was so extremely high as to compensate for its empirical implausibility. For instance, if we compare T with a rival theory T*, which asserts that the average entropy in the universe as a whole is about the same as the entropy of the region we observe, then in light of the preceding argument we have to acknowledge that T* is much more likely to be true, unless our prior probability function was severely biased towards T. (The bias would have to be truly extreme. It would not suffice, for example, if one’s prior probabilities where Pr(T) = 99.999999% and Pr(T*) = 0.000001%.) This vindicates the objection against Boltzmann. His anthropic explanation is refuted – probabilistically but with extremely high probability – by a more careful application of the anthropic principle. His account should therefore be modified or given up in favor of some other explanation.

Sklar thinks that the Boltzmannian has a "reasonable reply" (p.299) to this objection, namely that in Boltzmann's picture there will be some large regions where entropy is low, so our observations are not really incompatible with his proposal. However, while there is no logical incompatibility, the probabilistic incompatibility is of a very high degree. This can for all practical purposes be just as decisive as a logical deduction of a falsified empirical consequence, making it totally unreasonable to accept this reply.

            Sklar goes on to state what he seems to see as the real problem for Boltzmannians:

 

The major contemporary objection to Boltzmann’s account is its apparent failure to do justice to the observational facts. … as far as we can tell, the parallel direction of entropic increase of systems toward what we intuitively take to be the future time direction that we encounter in our local world seems to hold throughout the universe." (p. 300)

 

It is easy to see that this is just a veiled reformulation of the objection discussed above. If there were a "reasonable reply" to the former objection, the same reply would work equally well against this reformulated version. The Boltzmannian could simply retort by saying "Hey, even on my theory there will be some regions and some observers in those regions for whom, as far as they can tell, entropy seems to be on the increase throughout the universe – they see only their local region of the universe after all. Hence our observations are compatible with my theory!". If we are not impressed by this reply, it is because we are willing to take probabilistic entailments seriously. And failing to do so would spell methodological disaster for any theory that postulates a sufficiently big cosmos, since according to such theories there will always be some observer somewhere who observes what we are observing, so the theories would be logically compatible with any observation we could make.[32] But that is clearly not how such theories work.

SSA in evolutionary biology

Anthropic reasoning has been applied to estimate probabilistic parameters in evolutionary biology. For example, we may put the question how difficult it was for intelligent life to evolve on our planet.[33] Naively, one may think that since intelligent life evolved on the only planet we have closely examined, evolution of intelligent life seems quite easy. Science popularizer Carl Sagan seems to have held this view: "the origin of life must be a highly probable circumstance; as soon as conditions permit, up it pops!" (Sagan 1995). A moment’s reflection reveals that this inference is incorrect, since no matter how unlikely it was for intelligent life to develop on any given planet, we should still expect to have originated from a planet where such an improbable sequence of events took place. As we saw in chapter 2, only hypotheses according to which the difficulty of evolving intelligent life is so great that they give a small likelihood to there being even a single planet with intelligent life in the whole world are disfavored by the fact that intelligent life exists here.

Brandon Carter (Carter 1983, Carter 1989) combines this realization with some additional assumptions and argues that the chance that intelligent life will evolve on given Earth-like planet is in fact very small. His argument is outlined in this footnote.[34] Patrick Wilson (Wilson 1994) advances some objections against Carter’s reasoning, but as these objections do not concern the basic anthropic methodology that Carter uses they don’t need to be discussed here.

Carter has also suggested a clever way of estimating the number of improbable "critical" steps in the evolution of humans. The easiest way to grasp the idea may be through a little story. A princess is locked in a tower. Suitors have to pick five combination locks to get to her, and they can do this only through random trial and error, i.e. without memory of which combinations they have tried. A suitor gets one hour to pick all five locks. If he doesn’t succeed within the allotted time, he is shot. However, the princess’ charms are such that there is an endless string of suitors lined up and waiting for their turn.

After the deaths of some unknown number of suitors, one of them finally passes the test and marries the princess. Suppose that the numbers of possible combinations in the locks are such that the expected time to pick each lock is .01, .1, 1, 10, and 100 hours respectively. Suppose that pick-times for the suitor who got through are (in hours) {.00583, .0934, .248, .276, .319}. By inspecting this set you could reasonably guess that .00583 hour was the pick-time for the easiest lock and .0934 hour the pick-time for the second easiest lock. However, you couldn’t really tell which locks the remaining three pick-times corresponds to. This is a typical result. When conditioning on success before the cut-off (in this case 1 hour), the average completion time of a step is nearly independent of its expected completion time provided the expected completion time is much longer than the cut-off. Thus, for example, even if the expected pick-time of one of the locks had been a million years, you would still find that its average pick-time in successful runs is closer to .5 than to 1 hour.

If we don’t know the expected pick-times or the number of locks that the suitor had to break, we can obtain estimates of these parameters if we know the time it took him to reach the princess. The less time left before the cut-off, the greater the number of difficult locks he had to pick. For example, if the successful suitor took 59 minutes to get to the princess, then that would favor the hypothesis that he had to pick a fairly large number of locks. If he reached the princess in 35 minutes, that would strongly suggest that the number of difficult locks was quite small. The relation also works the other way around so that if we are not sure what is the maximum allowed time then we can use information about the time left over and the number of difficult locks to estimate it. Monte Carlo simulations confirming these intuitions can be found in (Hanson 1998), which also derives some analytical expressions.

            Carter applies these mathematical ideas to evolutionary theory by noting that an upper bound on the cut-off time after which intelligent life could not have evolved on Earth is given by the duration of the main sequence of the sun – about 10*10⁹ years. It took about 4*10⁹ years for intelligent life to develop. From this (together with some other assumptions which are problematic but not in ways relevant for our purposes) Carter concludes that the number of critical steps in human evolution is likely very small – not much greater than two.

One potential problem with Carter’s argument is that the duration of the main sequence of the sun only gives an upper bound on the cut-off; maybe climate change or some other type of event would have made Earth unconducive to evolution of higher organisms long before the sun becomes a red giant. Recognizing this possibility, Barrow and Tipler (Barrow and Tipler 1986) apply Carter’s reasoning in the opposite direction and seek to infer the true cut-off time by directly estimating the number of critical steps.[35] In a recent contribution, Robin Hanson (Hanson 1998) scrutinizes Barrow and Tipler’s suggestions for what are the critical steps and argues that their model does not fit the evidence very well when considering the relative time the various proposed critical steps actually took to complete.

            Our concern here is not which estimate is correct or even whether at the current state of biological science enough empirical data or theoretical understanding is available to supply the substantive premises needed to derive any specific conclusion from the sort of considerations described in this section.[36] My contention, rather, is twofold. Firstly, that if one wants to argue about or make a claim regarding such things as the improbability of intelligent life evolving, or the probability of finding extraterrestrial life, or the number of critical steps in human evolution, or the planetary window of opportunity during which evolution of intelligent life is possible, then one has to make sure that one’s position is coherent. Carter and others’ work in this area reveals subtle ways in which some views on these things are probabilistically incoherent. Secondly, that underlying the basic constraints appealed to in Carter’s reasoning (and this is quite independent of the specific empirical assumptions he needs to get any concrete results) is an application of SSA. WAP and SAP are inadequate in these applications. SSA makes its entrée when we realize that in a big cosmos there will be actual evolutionary histories of most any sort. On some planets, life will evolve very quickly; on others it will use up all the time available before the cut-off.[37] On some planets, difficult steps will be completed more quickly than easy steps. Without some probabilistic connection between the distribution of evolutionary histories and our own observed evolutionary past, none of the above considerations would even make sense.

            SSA is not the only methodological principle that would establish such a connection. For example, we could formulate a principle stating that every civilization should reason as if it were a random sample from the set of all civilizations. For the purposes of the above anthropic arguments in evolution theory this principle would amount to the same thing as the SSA, provided that all civilizations contained the same number of observers. However, when considering hypotheses on which certain types of evolutionary histories are correlated with the evolved civilizations containing a greater or smaller number of observers, this principle is not valid. We would then have to take recourse to the more general principle given by SSA.

SSA and traffic planning

When driving on the motorway, have you ever wondered about – or cursed – the phenomenon that cars in the other lane appear to be getting ahead faster than you? Although one may be inclined to account for this by invoking Murphy’s Law[38], a recent paper in Nature (Redelmeier and Tibshirani 1999) seeks a deeper explanation.

The authors argue that drivers are prone to change lanes on the motorway more often than they ought to because of various illusions which cause them to believe that the other lane is moving faster. For example, "a driver is more likely to glance at the next lane for comparison when he is relatively idle while moving slowly"; "Differential surveillance can occur because drivers look forwards rather than backwards, so vehicles that are overtaken become invisible very quickly, whereas vehicles that overtake the index driver remain conspicuous for much longer"; and "human psychology may make being overtaken (losing) seem more salient than the corresponding gains". The authors suggest that educating drivers about these effects might encourage them to resist small temptations to switch lanes, reducing the risk of accidents.

While not denying that these illusions might occur (see e.g. (Snowden, Stimpson et al. 1998, Walton and Bathurst 1998, Tversky and Kahneman 1981, Tversky and Kahneman 1991, Larson 1987, Angrilli, Cherubini et al. 1997, Gilovich, Vallone et al. 1985, Feller 1966)), I suggest that there is a more straightforward explanation, based on SSSA, why the other lane often appears faster. It goes as follows. One cause of why a lane (or a segment of a lane) is moving slowly is that there are too many cars in it. Even if the ultimate cause is something else (e.g. road works) there will nonetheless typically be a negative correlation between the speed of a lane and how densely packed are vehicles driving in it. That implies that a disproportionate fraction of drivers’ observer-moments are in slow-moving lanes. By SSSA, each observer-moment of a driver should therefore assign a correspondingly large probability to finding themselves in a slow-moving lane. In other words, appearances are faithful: more often than not, the "other" lane is faster.

The authors of the Nature article make a related point:

 

drivers are responding to an illusion: namely, that the next lane on a congested road appears to be moving faster than the driver’s present lane, even when both lanes have the same average speed. This occurs because vehicles spread out when moving quickly and pack together when moving slowly. A driver can therefore overtake many vehicles in a brief time interval, but it takes much longer for the driver to be overtaken by the same vehicles.

 

What is relevant to a driver who wants to get to her destination as quickly as possible, however, is not the average speed of the lane as a whole, but rather the speed of the lane in some segment extending maybe a couple of miles forwards from the driver’s present position. SSSA gives reason to think that more often than not, the other lane has a higher average speed at this scale than does the driver’s present lane. On average, there would therefore be some advantage to changing lanes (which of course has to be balanced against the cost of doing so in terms of increased levels of effort and risk).[39]

Summary

Through a series of gedanken we argued for reasoning in accordance with SSA in a wide range of cases. We showed that while the problem of the reference class is sometimes irrelevant when all hypotheses under consideration imply the same number of observers, the definition of the reference class becomes crucial when different hypotheses entail different numbers of observers. In those cases, what probabilistic conclusions we can draw depends on what sort of things are included in the reference class, even if the observer doing the reasoning knows that she is not one of the contested objects. We argued that many types of entities should be excluded from the reference class (stones, bacteria, buildings, plants etc.). We also showed that variations in regard to many quite "deep-going" properties (such as gender, genes, social status etc.) are not sufficient grounds for discrimination when determining membership in the reference class. Observers differing in any of these respects can at least in some situations belong to the same reference class.

            A complementary set of arguments focused on how SSA gives methodological guidance in a range of practical applications. These include:

 

·        Deriving observational predictions from contemporary cosmological models.

·        Evaluating a common objection against Boltzmann’s proposed thermodynamic explanation of time’s arrow.

·        Identifying probabilistic coherence constraints in evolutionary biology relevant when asking questions about the likelihood of intelligent life evolving on an Earth-like planet, the number of critical steps in human evolution, the existence of extraterrestrial intelligent life, and the cut-off time after which the evolution of intelligent life would no longer have been possible on Earth.

·        Analyzing claims about perceptual illusions among drivers.

·        And more.[40]

 

Any proposed rival to SSA would have to be checked in all the above thought experiments and practical applications. I challenge those who would reject SSA to propose a simpler or more plausible method of connecting such models to observational data. Something is clearly needed, since (for instance) big-universe models are so central in contemporary science.

            We proposed SSSA as a way of strengthening of SSA. Some open ends remain and no claim is made that SSSA represents the strongest possible correct rule for reasoning under observational selection effects. Yet, already SSA by itself is quite a lot. We shall now see that SSA is a very powerful principle that can carry unexpected consequences up its sleeve. For example, by making just a few seemingly quite weak additional assumptions, SSA leads directly to the Doomsday argument…

CHAPTER 5: THE DOOMSDAY ARGUMENT

Introduction

We have seen several examples where SSA gives intuitively plausible results. However, when SSA is applied to our actual situation and the future survival prospects of the human species, we get interesting consequences that we might not have anticipated. Coupled with a few seemingly quite weak empirical assumptions, SSA generates the Doomsday argument (DA), which purports to show that the life expectancy of the human species is less than one previously thought. This finding by itself might not be very startling. What makes DA shocking is, first, that this prediction is derived from premises which one might have thought too weak to entail such a thing. And second, that under certain not so implausible empirical assumptions the reduction in our species’ life expectancy is quite dramatic. The majority of people who hear about DA at first think there must be something wrong with it. A small but significant minority think it is obviously right.[41] What everybody must agree is that if the argument works then it would be an extremely important result. It would have major empirical consequences for an issue that we care a lot about: our survival.

            Many attempts have been made to refute DA. So far, such efforts have been unsuccessful. The next chapter will analyze in detail some of the more recent objections, and we shall see why they all fail. In this chapter we shall spell out the Doomsday argument, identify its assumptions, and examine various related issues. Looking at how the argument has been presented in the literature, we can identify two distinct forms of it, one due to Richard Gott and one to John Leslie (who is building on ideas by Brandon Carter). Gott’s version is incorrect. Leslie’s version, while a great improvement on Gott’s, also falls short on several points. Correcting these shortcomings does not, however, destroy the basic idea of the argument.

            DA has been independently discovered many times over. Brandon Carter was first, but he has not published on the issue. The credit for being the first person to clearly enunciate it in print belongs to John Leslie (Leslie 1989) who had heard rumors of Carter’s discovery from Frank Tipler. Leslie has been by far the most prolific writer on the topic with one monograph and over a dozen academic papers. Richard Gott III independently discovered and published a version of DA in 1993 (Gott 1993).[42] The argument also appears to have been conceived by H.B. Nielsen (Nielsen 1981 (although Nielsen might have been influenced by Tipler), and again more recently by Stephen Barr. Saar Wilf (personal communication) has convinced me that he too independently discovered the argument a few years ago. Although Leslie has the philosophically most sophisticated exposition of DA, it is instructive to first take a look at the version expounded by Gott.

Doomsday à la Gott

Gott’s version of DA is set forth in a paper in Nature dating from 1993 (Gott 1993; see also the responses Buch 1994, Goodman 1994, Mackay 1994, and Gott’s replies Gott 1994). A popularized exposition by Gott appeared in New Scientist in (Gott 1997). In the original article Gott not only sets forth a version of DA but he also pursues its implications for the search of extraterrestrial life project and for the prospects of space travel. Here we focus on what he has to say about DA.

Gott’s version is based on a more general argument type which he calls the "delta t argument". Notwithstanding its extreme simplicity, Gott reckons it can be used to make predictions about most everything in heaven and on earth. It goes as follows.

            Suppose we want to estimate how long some series of observations (or "measurements") is going to last. Then,

 

Assuming that whatever we are measuring can be observed only in the interval between times t_begin and t_end, if there is nothing special about t_now we expect t_now to be randomly located in this interval. (Gott 1993, p. 315)

 

Using this randomness assumption, we can make the estimate

 

.

 

t_future is the estimated value of how much longer the series will last. This means that we make the estimate that the series will continue for as long as it has already lasted when we make the random observation. This estimate will overestimate the true value half of the time and underestimate it half of the time. It also follows that a 50% confidence interval is given by

 

,

 

and a 95% confidence interval is given by

 

.

 

Gott gives some illustrations of how this reasoning can be applied in the real world:

 

[In] 1969 I saw for the first time Stonehenge () and the Berlin Wall (). Assuming that I am a random observer of the Wall, I expect to be located randomly in the time between t_begin and t_end (t_end occurs when the Wall is destroyed or there are no visitors left to observe it, whichever comes first). (Gott 1993, p. 315)

 

At least in these two cases, the delta t argument seems to have worked! The popular exposition in New Scientist article also features an inset inviting the reader to use the arrival date of that issue of the magazine to predict how long their current romantic relationship will last. You can presumably use my dissertation for the same purpose. How long has your present relationship lasted? Use that value for t_past and you get your prediction from the expressions above, complete with precisely specified confidence intervals.

            Wacky? Yes, but all this does indeed follow from the assumption that t_now is randomly (and uniformly) sampled from the interval t_begin to t_end. Gott admits that this imposes some restrictions on the applicability of the delta t argument:

 

[At] a friend’s wedding, you couldn’t use the formula to forecast the marriage’s future. You are at the wedding precisely to witness its beginning. Neither can you use it to predict the future of the Universe itself – for intelligent observers emerged only long after the Big Bang, and so witness only a subset of its timeline. (Gott 1997, p. 39)

 

Unfortunately, Gott does not discuss in any more detail the all-important question of when, in practice, the delta t argument is applicable. Yet it is clear from his examples that he thinks it should be applied in a very broad range of real-world situations.

In order to apply the delta t argument to estimate the life-expectancy of the human species, we must measure time on a "population clock" where one unit of time corresponds to the birth of one human. This modification is necessary because the human population is not constant. Thanks to population growth, most humans that have been born so far find themselves later rather than earlier in the history of our species. According to SSA, we should consequently assign a higher prior probability to finding ourselves at these later times. By measuring time as the number of humans that have come into existence, we obtain a scale where you can assign a uniform sampling density to all points of time.

            There has been something like 60 billion humans so far. Using this value as t_past, the delta t argument gives the 95% confidence interval

 

.

 

            The units are human births. In order to convert this to years, we would have to estimate what the future population figures will be given that a total of N humans will have existed. In the absence of such an estimate, DA leaves room for alternative interpretations. If the world population levels out at 12 billion and human life-expectancy stabilizes at approximately 80 years then disaster is likely to put an end to our species fairly soon (within 1200 years with 75% probability). If population figures rise higher, the prognosis is even worse. But if population decreases drastically or individual human life-spans get much longer, then the delta t argument would be compatible with survival for millions of years.

            The probability of space colonization looks dismal in the light of Gott’s version of DA. Reasoning via the delta t argument, Gott concludes that the probability that we will colonize the galaxy is about , because if we did manage such a feat we would expect there to be at least a billion times more humans in the future than have been born to date.

The incorrectness of Gott’s argument

A crucial flaw in Gott’s argument is that it fails to take into account our empirical prior probability of the hypotheses under consideration. Even granting that SSA is applicable to all the situations and in the manner that Gott suggests (and we shall argue in a later chapter that that is not generally the case, because the "no-outsider requirement" is not satisfied), the conclusion would not necessarily be the one intended by Gott once this omission is rectified.

            And it is quite clear, once we focus our attention on it, that our prior probabilities must be considered. It would be foolish when estimating the future duration of Stonehenge or the Berlin wall not to take into account any other information you might have. Say you are part of a terrorist organization bent on destroying Stonehenge to get publicity. Everything has been carefully plotted: the explosives are in the truck, the detonators are in your suitcase; tonight at 11 p.m. your two co-conspirators will to pick you up from King’s Cross St. Pancras… Knowing this, surely the odds of Stonehenge lasting another year are different from and lower than what a straightforward application of the delta t argument would suggest. In order to save the delta t argument, Gott would have to restrict its applicability to situations where we in fact lack other relevant information. But then the argument cannot be used to estimate the future longevity of the human species, because we certainly have plenty of extraneous information that is relevant to that. So Gott’s version of DA fails.

            That leaves open the question whether the delta t argument might not perhaps provide interesting guidance in some other estimation problems. Suppose we are trying to guess the future duration of some phenomenon and that we have a "prior" probability distribution (after taking into account all other empirical information available) that is uniform for total duration T in the interval , and is zero for T > T_max:

 

           

Suppose you make an observation at a time t₀ and find that the phenomenon at that time has lasted for (t₀ - 0) (and is still going on). Let us assume further, that there is nothing "special" about the time you choose to make the observation. That is, we assume that the case is not like using the delta t argument to forecast the prospects of a friend’s marriage at his wedding. We have made quite a few assumptions here, but if the argument could be shown to work under these conditions it might still find considerable practical use. Some real-world cases at least approximate this ideal setting.

            Even under these conditions, however, the argument is inconclusive because it neglects an important observational selection effect. The probability that your observation should occur at a time when the phenomenon is still ongoing is greater the longer the phenomenon lasts. Imagine that your observation occurs in two steps. First, you discover that the phenomenon is still in progress. Second, you discover that it has lasted for (t₀ - 0). After the first step, you may conclude that the phenomenon probably lasts longer than your prior probability led you to expect; for it is more likely that you should observe it still in progress if it covers a greater time interval. This is true if we assume that your observation was made at a random point in a time interval that is longer than the expected duration of the phenomenon. The longer the time interval from which the observation point is sampled compared to the prior expected duration of the phenomenon, the stronger the influence that this observational selection effect will have on the posterior probability. In particular, it will tend to compensate for the "Doomsday-effect" – the tendency which finding that the phenomenon has lasted only a short time when you make the observation has to make you think that the duration of the phenomenon is relatively short. We will show this in more mathematical detail when we study the no-outsider requirement in the next chapter. For now, it suffices to note that if your observation is sampled from a time interval that is longer than the minimum guaranteed duration of the phenomenon – so that you could have made your observation before the phenomenon started or after it had ended – then finding that the phenomenon is still in progress when you make your observation gives you some reason to think that the phenomenon probably lasts for a relatively long time. The delta t argument fails to take account of this effect. The argument is hence flawed, unless we make the additional assumption (not made by Gott) that your observation point is sampled from a time interval that does not exceed the duration of the phenomenon. And this entails that in order to apply Gott’s method, you must be convinced that your observation point’s sampling interval co-varies with durations of the phenomenon. That is to say, you must be convinced that given the phenomenon lasts from t_a to t_b, then your observation point is sampled from the interval [t_a, t_b]; and that given that the phenomenon lasts from t_a’ to t_b’, then your observation point is sampled from the interval [t_a’, t_b’]; and similarly for any other start- and end-points that you assign a non-zero prior probability. This imposes a strong additional constraint on situations where the delta t argument is applicable.[43]

            The failure of Gott’s approach to take into account the empirical prior probabilities and to respect the no-outsider requirement constitute the more serious difficulties with the "Copernican Anthropic Principle" alluded to in chapter 3 and are part of the reason why we replaced that principle with SSA.

Doomsday à la Leslie

Leslie’s presentation of DA differs in several respects from Gott’s. On a stylistic level, Leslie makes less use of mathematics, his writing is informal and his arguments often take the form of analogies. Leslie is much more explicit than Gott about the philosophical underpinnings. He places the argument in a Bayesian framework and devotes considerable attention to the empirical considerations that determine what the priors are as well as to the ethical issues related to seeking to minimize the risk of human extinction.

            Leslie presents DA through a loosely arranged series of gedanken and analogies. A large part of the argumentation consists in refuting various objections that could be advanced against the proposed line of reasoning. This makes it difficult to briefly summarize Leslie’s version of DA in a way that does justice to it, but a characteristic passage runs as follows:

 

One might at first expect the human race to survive, no doubt in evolutionary much modified form, for millions or even billions of years, perhaps just on Earth but, more plausibly, in huge colonies scattered through the galaxy and maybe even through many galaxies. Contemplating the entire history of the race – future as well as past history – I should in that case see myself as a very unusually early human. I might well be among the first 0.00001 per cent to live their lives. But what if the race is instead about to die out? I am then a fairly typical human. Recent population growth has been so rapid that, of all human lives lived to far, anything up to about 30 per cent ... are lives which are being lived at this very moment. Now, whenever lacking evidence to the contrary one should prefer to think of one’s own position as fairly typical rather than highly untypical. To promote the reasonable aim of making it quite ordinary that I exist where I do in human history, let me therefore assume that the human race will rapidly die out. (Leslie 1990, pp. 65f; emphasis in original. )

 

            Leslie emphasizes the point that DA does not show that doom will strike soon. It only argues for a probability shift. If we started out being extremely confident that the humans species will survive for a long time, we might still be fairly confident after having taken DA into account – though less confident than before. Also, it is possible for us to improve our prospects. Leslie hopes that by convincing us that the risks are greater than was previously thought we will become more willing to take steps to diminish the dangers – perhaps by pushing for nuclear disarmament, setting up an early-warning system for meteors on collision course with Earth, being careful with future very-high-energy particle physics experiments (which could conceivably knock our cosmic region out of a metaunstable vacuum state and destroy the world), or preparing workable strategies for dealing with the coming impact of molecular nanotechnology (Drexler 1985, Drexler 1992, Freitas(Jr.) 1999). So Leslie does not see DA as a ground for despair, but rather as a call for greater caution and concern about potential species-annihilating disasters.

A major advantage of Leslie’s version compared to Gott’s is that Leslie explicitly stresses that the empirical priors must be taken into account. Bayes’ theorem tells us how to do that. Suppose we are entertaining two hypotheses about how many humans there will have been in total:

 

H₁: There will have been a total of 200 billion humans.

H₂: There will have been a total of 200 trillion humans.

 

For simplicity, let’s assume that these are the only possibilities. The next step is to assign prior probabilities to these hypotheses based on the empirical information available (but ignoring, for the moment, information about your birth rank). For example, you might think that:

 

P(H₁) = 5%

P(H₂) = 95%

 

All that remains now is to factor in the information about your birth rank, which, as it happens, is somewhere in the neighborhood of 60 billion (R) if you are alive in the beginning of the 21^st century.

 

          (#)

 

In this illustration, the prior probability of Doom soon (H₁) of 5% is increased to about 98% when you take into account your birth rank according to DA. This is how Leslie envisions that calculations based on his version are to be made.

Note however that the calculation is not the argument. Rather, the calculation is a derivation of a specific prediction from assumptions which DA seeks to justify. Let’s look in more detail at what these assumptions are and whether they can be supported.

The assumptions used in DA, and the Old evidence problem

Leslie talks of the principle that, lacking evidence to the contrary, one should think of one’s position as "fairly typical rather than highly untypical". In chapter 3, we proposed to tidy up this rather imprecise idea by explicating it as SSA. In chapter 4, we provided grounds for adopting SSA in a range of cases. The crucial question is, can SSA be applied in the context of DA in the way the above calculation presupposes?

            Let’s suppose for a moment that it can. What other assumptions does the argument use? Well, an assumption was made about the prior probabilities of H₁ and H₂. This assumption is no doubt incorrect, since there are other hypotheses that we want to assign non-zero probability. However, it is clear that choosing different values of the prior will not change the fact that hypotheses which postulate fewer observers will gain probability relative to hypotheses which postulate more observers.[44] The absolute posterior probabilities depend on the precise empirical prior but the fact that there is this probability shift does not. Further, (#) is merely a formulation of Bayes’ theorem. So once we have the empirical priors and the conditional probabilities, the prediction follows mathematically.

            The premiss that bears the responsibility for the surprising conclusion is the idea that SSA can be applied to justify these conditional probabilities. Can it?

            Recall that we argued for Model 2 in the first version (G1) of God’s Coin Toss in chapter 4. If DA could be assimilated to this case, it would be justified to the extent that we accept Model 2. The cases are in some ways similar, but there are also a number of differences. The question is whether the differences are relevant. This section studies the extent to which the arguments that were made in favor of Model 2 can be adapted to support DA. We will find that there are significant disanalogies between the two cases. It might be possible to bridge these disanalogies, but until that is done the attempt to support the assumptions of DA by assimilating it to something like Model 2 for God’s Coin Toss remain inconclusive. This is not to say that the similarities between the two cases cannot be persuasive for some people. So this section is neither an attack on nor a defense of DA. (On the other hand, in chapter 8 we will find that the reasoning used in Model 2 leads to quite strongly counterintuitive results and in chapter 9 we will develop a new way of thinking about cases like God’s Coin Toss which need not lead to DA-like conclusions. Those results will suggest that even if we are persuaded that DA could be assimilated to Model 2, we may still not accept DA because we reject Model 2!)

One argument that was used to justify Model 2 for G1 was that if you had at first been ignorant of the color of your beard, and you had assigned probabilities to all the hypotheses in this state of ignorance, and you then received information about your beard color and updated your beliefs in accordance with Bayes’ theorem, then you would end up with the probability assignments that Model 2 prescribes. This line of reasoning does not presuppose that you actually were, at some point in time, ignorant of your beard color. Rather, considering what you would have thought if you had been once ignorant of the beard color is merely a way of clarifying your current conditional probabilities of being in a certain room given a certain outcome of God’s coin toss.

I hasten to add that I am not suggesting a counterfactual analysis as a general account of conditional degrees of belief. That is, I am not saying that P(e|h) should in general be defined as the probability you would have assigned to e if you didn’t know e but knew h. A solution of the so-called old evidence problem (see e.g. (Earman 1992, Schlesinger 1991, Achinstein 1993, Howson 1991, Eells 1990) requires something rather more subtle than that. However, thinking in terms of such counterfactuals can in some cases be a useful way of getting clearer about what your subjective probabilities are. Take the following case.

 

Two indistinguishable urns are placed in front of Mr. Jonas. He is credibly informed that one of them contains ten balls and the other a million balls, but he is ignorant as to which is which. He knows the balls in each urn are numbered consecutively 1, 2, 3, 4… and so on. Jonas flips a coin which he is convinced is fair, and based on the outcome he selects one of the urns – as it happens, the left one. He picks a ball at random from this urn. It is ball number 7. Clearly, this is a strong indication that the left urn contains only ten balls. If originally the odds were fifty-fifty (which is reasonable given that the urn was selected randomly), a swift application of Bayes’ theorem gives the posterior probability that the left urn is the one with only ten balls: Pr(Left urn contains 10 balls | Sample ball is #7) = 99.999%.

Mr. Jonas, however, was never a man of proclivity for intellectual exercises. When he picks the ball with number 7 on it and is asked to give his odds for that urn being the one with only ten balls, he says: "Umm, fifty-fifty!"

 

Before Mr. Jonas stakes his wife’s car on these inclement odds, what can we say to him to help him come to his senses? When we start explaining about conditional probabilities, Jonas decides to stick to his guns rather than admit that his initial response is incorrect. He accepts Bayes’ theorem, and he accepts that the probability that the ten-ball urn would be selected by the coin toss was 50%. What he refuses to accept is that the conditional probability of selecting ball number 7 is one in ten (one in a million), given that the urn contains ten (one million) balls. Instead he thinks that there was a 50% probability of selecting ball number 7 on each hypothesis about the total number of balls in the urn. Or maybe he declares that he simply doesn’t have any such conditional credence.

One way to proceed from here is to ask Jonas, "What probability would you have assigned to the sample you have just drawn being number 7 if you hadn’t yet looked at it but you knew that it had been picked from the urn with 10 balls?" Suppose Jonas say, "One in ten." We may then appropriately ask, "So why then does not your conditional probability of picking number 7 given that the urn contains ten balls equal one in ten?".

There are at least two kinds of reasons that one could give to justify a divergence of one’s conditional probabilities from what one thinks one would have believed in a corresponding counterfactual situation. First, one may think that one would have been irrational in the situation in question. What I think I would believe in a counterfactual situation where I was drugged into a state of irrationality can usually be ignored for the sake of determining my current conditional probabilities.[45] In the case of Jonas this response is not available, because Jonas does not believe he would have been irrational in the counterfactual situation where he hadn’t yet observed the number on the selected ball; in fact, let’s suppose, Jonas thinks he would have believed the only thing that would have been rational for him to believe.

            A second reason for divergence is if the counterfactual situation (where one doesn’t know e) doesn’t exactly "match" the conditional probability P(e|h) being assessed. The corresponding counterfactual situation might contain features – other than one’s not knowing e – that would rationally influence one’s degree of belief in h. For instance, suppose we add the following feature to the example: Mr. Jonas has been credibly informed at the beginning of the experiment that if there is a gap in time ("Delay") between the selection of the ball and his observing what number it is (so that he has the opportunity to be for a while in a state of ignorance as to the number of the selected ball) then the experiment has been rigged in such a way that he was bound to have selected either ball number 6 or 7. Then in the counterfactual situation where Jonas is ignorant of the number on the selected ball, Delay would be true; and Jonas would have known that. In the counterfactual situation he would therefore have had the additional information that the experiment was rigged (an event to which, we can assume, he assigned a low prior probability). Clearly, what he would have thought in that counterfactual situation does not determine the value that he should in the actual case assign to the conditional probability P(e|h), since in the actual case (where Delay is false) he does not have that extra piece of information. (What he thinks he would have thought in the counterfactual situation would rather be relevant to what value he should presently give to the conditional probability P(e|h&Delay); but that is not what he needs to know in the present case.)

            This second source of divergence suggests a more general limitation of the validity of the counterfactual-test of what your current conditional probabilities should be. In many cases, there is no clearly defined unique situation that would have obtained if you had not known some data that you in fact know. There are many ways of not knowing something. Take the counterfactual situation, for example, where I don’t know whether clouds ever exist. Is that a situation where I don’t know that there is a sky and a sun (so that I don’t know whether clouds ever exist because I have never been outdoors and looked to the sky)? Is it a situation where I don’t know how water in the air behaves when it is cooled down? Or is it perhaps a situation where I am ignorant as to whether the fluffy things I see up there are really clouds rather than, say, gods made out of cotton? Is it one where I have never been up in an airplane and thus never seen clouds up close? Or one where I have flown but have forgotten about some parts of the experience? It seems clear that we have not specified the hypothetical state of "me not knowing whether clouds have ever existed" sufficiently to get an unambiguous answer to what else I would or would not believe if I were in that situation.

In some cases, however, the counterfactual situation is sufficiently specified. Take the original case with Mr. Jonas again (where there is no complication such as the selection potentially being rigged). Is there a counterfactual situation that we can point to as the counterfactual situation that Jonas would be in if he didn’t know the number on the selected ball? It seems there is. Suppose that in the actual course of the experiment there was a one-minute interval of ignorance between Jonas’ selecting a ball and his looking to see what number it was. Suppose that during this minute Jonas contemplated his probability assignments to the various hypotheses and reached a reflective equilibrium. Then one can plausibly maintain that, at the later stage when Jonas have looked at the ball and knows its number, what he would have rationally believed if he didn’t know its number is what he did in fact believe a moment earlier before he learnt what the number is. Moreover, even if in fact there never were an interval of ignorance where Jonas didn’t know e, it can still make sense to ask what he would have thought if there had been. At least in this kind of example there can be a suitably definite counterfactual from which we can read off what conditional probability P(e|h) Jonas was once implicitly committed to.

If this is right, then there are at least some cases where the conditional credence P(h|e) can be meaningfully assigned a non-trivial probability even if there never in fact was any time when e was not known. The old evidence problem retains its bite in the general case, but in some special cases it can be tamed. This is indeed what one should have expected since otherwise the Bayesian method could never be applied except in cases where one had in advance contemplated and assigned probabilities to all relevant hypotheses and possible evidence. That would fly in the face of the fact that we are often able to plausibly model the evidential bearing of old evidence on new hypotheses within a Bayesian framework.

Returning now to the God’s Coin Toss (G1) gedanken, we recall that it was not assumed that there actually was a point in time when the people created in the rooms were ignorant about the color of their beards. They popped into existence, we could suppose, right in front of the mirror, and gradually came to form a system of beliefs as they reflected on their circumstances.[46] Nonetheless we could use an argument involving a counterfactual situation where they were ignorant about their beard color to motivate a particular choice of conditional probability. Let’s look in more detail at how that could be done.

I suggest that the following is the right way to think about this. Let I be the set of all information that you have received up to the present time. I can be decomposed in various ways. For example, if I is logically equivalent to I₁&I₂ then I can be decomposed into I₁ and I₂. You currently have some credence function which specifies your present degree of belief in various hypotheses (conditional or otherwise), and this credence is conditionalized on the background information I. Call this credence function C_I. However, although this is the credence function you have, it may not be the credence function you ought to have. You may have failed to understand all the probabilistic connections between the facts that you have learnt. Let C_I^* be a rival credence function, conditionalized on the same information I. The task is now to try to determine whether on reflection you ought to switch to C_I^* or whether you should stick with C_I.

The relation to DA should be clear. C_I can be thought of as your credence function before you heard about the DA, and C_I^* the credence function that the proponent of DA (the "doomsayer") seeks to persuade you to adopt. Both these functions are based on the same background information I, which includes everything you have learnt up until now. What the doomsayer argues is not that she can teach you some new piece of relevant information that you didn’t have before, but rather that she can point out a probabilistic implication of information you already have that you hitherto failed to fully realize or take into account – in other words that you have been in error in assessing the probabilistic bearing of your evidence on hypotheses about how long the human species will last. How can she go about that? Since presumably you haven’t made any explicit calculations to decide what credence to attach to these hypotheses, she cannot point to any error you have made in some mathematical derivation. But I want to suggest one method she can use:

She can specify some decomposition of your evidence into I₁ and I₂. She can then ask you what you think you ought to have rationally believed if all the information you had were I₁ (and you didn’t know I₂). (This thought operation involves reference to a counterfactual situation, and as we saw above, whether such a procedure is legitimate depends on the particulars; sometimes it works, sometimes it doesn’t. Let’s assume for the moment that it works in the present case.) What she is asking for, thus, is what credence function C_I1 you think you ought to have had if your total information were I₁. In particular, C_I1 assigns values to certain conditional probabilities of the form C_I1(*|I₂). This means we can then use Bayes’ theorem to conditionalize on I₂ and update the credence function. If the result of this updating is C_I^*, then she will have shown that you are committed to revising your present credence function C_I and replace it by C_I^* (provided you choose to adhere to C_I1(*|I₂) even after realizing that this obligates you to change C_I). For C_I and C_I^* are based on the same information, and you have just acknowledged that you think that if you were ignorant of I₂ you should set your credence equal to C_I1, which results in C_I^* when conditionalize on I₂. One may summarize this, roughly, by saying that the order in which you choose to consider the evidence should not make any difference to the probability assignment you end up with.[47]

This method can be applied to the case of Mr. Jonas. I₁ is all the information he would have had up to the time when the ball was selected from the urn. I₂ is the information that this ball is number 7. If Mr. Jonas firmly maintains that what would have been rational for him to believe had he not known the number of the selected ball (i.e. if his information were I₁) is that the conditional probability of the selected ball being number 7 given that the selected urn contains ten balls (a million balls) is one in ten (one in a million), then we can show that his present credence function ought to assign a 99.999% credence to the hypothesis that the left urn, the urn from which the sample was taken, contains only ten balls.

In order for the doomsayer to use the same method to convince somebody who resists DA on the grounds that the conditional probabilities used in DA do not agree with his actual conditional probabilities, she’d have to define some counterfactual situation S such that the following holds:

 

(1) In S he does not know his birth rank.

(2) The probabilities assumed in DA are the probabilities he now thinks that it would be rational for him to have in S.

(3) His present information is logically equivalent to the information he would have in S conjoined with information about his birth rank (modulo information which he thinks is irrelevant to the case at hand).

 

The probabilities referred to in (2) are of two sorts. There are the "empirical" probabilities that DA uses – the ordinary kind of estimates of the risks of germ warfare, asteroid impacts, abuse of military nanotechnology etc. And then there are the conditional probabilities of having a particular birth rank given a particular hypothesis about the total number of humans that will have lived. The conditional probabilities presupposed by DA are the ones given by applying SSA to that situation. S should therefore ideally be a situation where he possesses all the evidence he actually has which is relevant to establishing the empirical prior probabilities, but where he lacks any indication as to what his birth rank is.

Can such a situation S be conceived? That is what is unclear. Consider the following initially beguiling but unworkable argument:

 

An erroneous argument

What if we in actual fact don’t know our birth ranks, even approximately? What if we actually are in this hypothetical state of partial ignorance which the argument for choosing the appropriate conditional probabilities presupposes? "But," you may object, "didn’t you say that our birth ranks are about 60 billion? And if I know that this is (approximately) the truth, how can I be ignorant about my birth rank?"

            Well, what I said was that your birth rank in the human species is about 60 billion. Yet that does not imply that your birth rank simpliciter is anywhere near 60 billion. There could be other intelligent species in the universe, extraterrestrials that count as observers, and I presume you would not assert with any confidence that your birth rank within this larger group is about 60 billion. You presumably agree that you are highly uncertain about your temporal rank in the set of all observers in cosmos, if there are many extraterrestrial civilizations out there.

            The appropriate reference class to which SSA is applied must include all observers that will ever have existed, and intelligent extraterrestrials – at least if they were not too dissimilar to us in other respects – should count as observers. The arguments of chapter 4 for adopting SSA work equally well if we include extraterrestrials in the reference class. Indeed, the arguments that were based on how SSA seems the most plausible way of deriving observational predictions from multiverse theories and of making sense of the objections against Boltzmann’s attempted explanation of the arrow of time presuppose this! And the arguments that were based on the thought experiments can easily be adapted to include extraterrestrials – draw antennas on some of the people in the illustrations and adjust the terminology accordingly, and these arguments go through as before.

We can consequently propose for the consideration of Mr. Jonas (who now plays the role of a skeptic about DA) the following hypothetical situation S (which might be a counterfactual situation or a situation that will actually occur in the future):

 

Scientists report that they have obtained evidence that strongly favors the disjunction , where h₁ is the hypothesis that our species is the only intelligent life-form in the world, and h₂ is the hypothesis that our species is one out of a total of one million intelligent species throughout spacetime, each of which is pretty much like our own in terms of constitution and membership numbers. (To avoid the complication that infinite population sizes introduces, we may also assume that it is known that the total number of observers that will have existed in the world is bound by some large but finite number.) Mr. Jones knows what his birth rank would be given h₁, namely about 60 billion; but he does not know even approximately what his birth rank would be given h₂. By considering various strings of additional incoming evidence favoring either h₁ or h₂ we can thus probe how he does or does not take into account the information about his birth rank in evaluating hypotheses about how long the human species will last. Suppose first that evidence comes in strongly favoring h₂. We then have a situation S satisfying the three criteria listed above. Mr. Jonas acknowledges that he is ignorant about his birth rank, and so he now thinks that in this situation it would be rational for him to apply SSA. This gives him the conditional probabilities required by DA. The empirical priors are, let us assume, not substantially affected by the information favoring h₂; so they are the same in S as they are in his actual situation. Suppose, finally, that scientists a while later and contrary to expectation obtain new evidence that very strongly favors h₁. When Jonas learns about this, his information set becomes equivalent to the information set he has in the actual situation (where we assume that Jonas does not believe there are any extraterrestrials). The input that the DA-calculation above needed are thus all supplied in this case, and Bayes’ theorem implies what Jonas’ posterior probability (after conditionalizing on his birth rank) should be.

 

It could seem as if we have described a hypothetical situation S that satisfies criteria (1) to (3) and thus verifies DA. Not so. The weakness of scenario is that although Jonas doesn’t know even approximately what his birth rank is in S, he still knows in S his relative birth rank within the human species: he is about the 60 billionth human. Thus he could maintain that when he applies SSA, he should assign probabilities that are invariant between various specifications of our species’ position among all the extraterrestrial species – since he is ignorant about that – but that the probabilities should not be uniform over various positions within the human species – since he is not ignorant about that. For example, if we suppose that the various species are temporally non-overlapping so that they exist one after another, then he might assign a probability close to one that his absolute birth rank is either about 60 billion, or about 120 billion, or about 180 billion, or… . Suppose this is what he now thinks it would be rational for him to do in S. Then the DA-calculation does not get the conditional probabilities it needs to give the intended conclusion, and DA fails. For after conditioning on the strong evidence for h₁, the conditional probability of having a birth rank of roughly 60 billion will be the same given any of the hypotheses about the total size of the human species that he might entertain.

It might be possible to construct some other hypothetical situation S that would really satisfy the three constraints, and that could thus serve to compel a person like Mr. Jonas to adopt the conditional probabilities that DA requires.[48] But until such a situation is described (or some other argument provided for why he should accept those probabilities), this is a loose end that those whose intuitions do not drive them to adopt the requisite probabilities without argument may gladly cling to.

Leslie on the problem with the reference class

How does Leslie answer the question of how the reference class should be determined? As a first remark, Leslie suggests that "perhaps nothing too much hangs on it." (Leslie 1996, p. 257):

 

[DA] can give us an important warning even if we confine our attention to the human race’s chances of surviving for the next few centuries. All the signs are that these centuries would be heavily populated if the race met with no disaster, and they are centuries during which there would presumably be little chance of transferring human thought-processes to machines in a way which would encourage people to call the machines ‘human’. (Leslie 1996, p. 258)

 

            This clearly not an entirely satisfying reply. First, the premise that there is little chance of creating machines with human-level and human-like thought processes within the next few centuries is something that many of those who have thought seriously about these things disagree with. Many thinkers in this field think that these developments will happen well within the first half of this century (e.g. Moravec 1989, Moravec 1998, Moravec 1999, Drexler 1985, Minsky 1994, Bostrom 1998, Bostrom and et al. 1999, Kurzweil 1999). Second, the comment does nothing to allay the suspicion that the difficulty of determining an appropriate reference class might be symptomatic of an underlying ill in DA itself.

            Leslie proceeds, however, to offer a positive proposal for how to settle the question of which reference class to choose.

            The first part of this proposal is best understood by expanding the urn analogy in which we first made the acquaintance of our friend Mr. Jonas. Suppose that the balls in the urns come in different colors. And suppose your task is to guess how many red balls there are in the left urn. Now, "red" is clearly a vague concept – what shades of pink or purple count as red? This vagueness could be seen as corresponding to the vagueness about what to classify as an observer for the purposes of DA. So, if some vagueness like this is present in the urn example, does that mean that the Bayesian induction used in the original example can no longer be made to work?

            By no means. The right response in this case is that you have a choice as to how you define the reference class. The choice depends on what hypothesis you are interested in testing. Suppose that what you are interested in finding out is how many balls there are in the urn of the color light-pink-to-dark-purple. Then all you have to do is to classify the random sample you select as being either light-pink-to-dark-purple or not light-pink-to-dark-purple. Once you have made this classification, the Bayesian calculation proceeds exactly as before. If instead you are interested in knowing how many light-pink-to-light-red balls there are, then you classify the sample according to whether it has that property, and proceed as before. The Bayesian apparatus is perfectly neutral as to how you define the hypotheses. There is not a right or wrong way, just different questions you might be interested in asking.

            Applying this idea to DA, Leslie writes:

 

The moral could seem to be that one’s reference class might be made more or less what one liked for doomsday argument purposes. What if one wanted to count our much-modified descendants, perhaps with three arms or with godlike intelligence, as ‘genuinely human’? There would be nothing wrong with this. Yet if we were instead interested in the future only of two-armed humans, or of humans with intelligence much like that of humans today, then there would be nothing wrong in refusing to count any others. (Leslie 1996, p. 260)

 

This suggests that if we are interested in the survival-prospects of just a special kind of observers, we are entitled to apply DA to this subset of the reference class. Suppose you are Asian and you want to know how many Asians there will have been. Answer: Count the number of Asians that have existed before you and use the DA-style calculation to update your prior probabilities (given by ordinary empirical considerations) to take account of the fact that this random sample from the set of all Asian – you – turned out to be living when just so many Asians had already been born.

            How far can one push this mode of reasoning though, before crashing into absurdity? If the reference class is defined to consist of all those people who were born on the same day as me or later, then I should expect doom to strike quite soon. Worse still, let’s say I want to know how many people there will have been with the property of being born either on the tenth of March in 1973 or being born after the year 2002. Since 10/3/73 is the day I was born, I will quickly become "improbably early" in this "reference class" if humans continue to be sired after 2002. Should I therefore have to conclude that humankind is very likely to go extinct in the first few weeks of 2003? Crazy!

How can the doomsayer avoid this conclusion? According to Leslie, by adjusting the prior probabilities in a suitable way, a route which he says was suggested to him by Carter (Leslie 1996, p. 262). Leslie thinks that defining the reference class as humans-born-as-late-as-you-or-later is fine and that ordinary inductive knowledge will make the priors so low that no absurd consequences will follow:

 

No inappropriately frightening doomsday argument will result from narrowing your reference class ... provided you adjust your prior probabilities accordingly. Imagine that you'd been born knowing all about Bayesian calculations and about human history. The prior probability of the human race ending in the very week you were born ought presumably to have struck you as extremely tiny. And that’s quite enough to allow us to say the following: that although, if the human race had been going to last for another century, people born in the week in question would have been exceptionally early in the class of those-born-either-in-that-week-or-in-the-following-century, this would have been a poor reason for you to expect the race to end in that week, instead of lasting for another century. (Leslie 1996, p. 262)

 

I disagree with the claim that the prior inductive improbability is enough to allow us to say this. That appealing to the inductive improbability will not do the job of compensating for phony choices of reference class follows logically from the fact that the inductive evidence (for the hypothesis that humankind will end in a given time interval, say within a week from now) is constant no matter how we define the reference class, whereas the reference class could be defined in arbitrarily many ways, thereby varying the strength of the resulting probability shift. The inductive evidence could "compensate" for at most one strength of the shift, while for all other choices of reference class, a different and incompatible prediction would result.

It is true that we can always choose the values that we plug into the variables representing the priors in the Bayesian formula in such a way that we reproduce the posterior probability resulting from the correct choice of reference class and priors. But these values that we plug in will not in general be prior probabilities. They will be mere numbers, chosen ad hoc because when inserted into Bayes' formula they happen to give the output we had decided in advance we wanted to get. Instead of Bayes’ formula we could have used any function onto the unit interval, or simply not bothered at all.

I conclude that the idea that it doesn’t matter how we define the reference class because we can compensate by adjusting the priors is misconceived. We saw in chapter 4 that the reference class must not be too wide – it must not include rocks for example. Now we have just seen that it must not be made too narrow either – for instance, by excluding all persons born earlier than yourself.

Between these boundaries there is still plenty of space for divergent definitions. Does this mean that there are many correct choices of reference class, and that context and what we are interested in predicting may determine which choice is appropriate in a given situation? Or should we suppose that there is only one legitimate reference class, albeit it has not yet been determined what it is and it might even be quite vague a matter at the end of the day?

The example in which an Asian applies DA to predict how many Asians there will have been may at first sight appear to work quite well; it seems no less plausible than applying DA to predict the total number of observers. I think it would be a mistake to take this as evidence that the reference class varies depending on what we are trying to predict. If the Asian-example works, it is only because one thinks there is no systematic relationship between Asians and observers in general. But suppose one thought otherwise. For example, suppose you were convinced that a racist madman had engineered and was planning to release a virus that will sterilize all Asians while leaving other ethnic groups intact. Suppose you thought on ordinary empirical grounds that the madman had a fifty percent chance of succeeding. Let’s also suppose that you were convinced that his success or failure would not have any significant effect on the total number of observers that will ever have lived (maybe other races would breed more to compensate for the loss of Asian fertility). Applying DA to this situation would not increase your probability that the madman would succeed, since his deed makes no difference to the total number of observers. If as an Asian you defined a reference class consisting of all Asians, and applied a DA-style inference scheme to that, you would get the result that the madman’s success was more likely than fifty percent. This prediction conflicts with the predictions from a straightforward application of DA, so at least one of them has to be wrong. The definition of the reference class, even omitting extreme measures such as including rocks or defining it with reference to the day you were born, cannot be arbitrary. For if DA is correct, it does not make inconsistent predictions.

Alternative conclusions of the Doomsday argument

It should be pointed out that even if DA is basically correct, there is still vast scope for alternative interpretations of the result other than that humankind is likely to go extinct soon. For example, one may think that:

·        The priors are so low that even after a substantial probability shift in favor of earlier doom, we are still likely to survive for quite a while.

·        The size of the human population will decrease in the future; this reconciles DA with even extremely long survival of the human species.

·        Humans evolve (or reengineer ourselves using advanced technology) into entities, posthumans, that belong in a different reference class than humans. All that DA would show in this case is that the posthuman transition is likely to happen before there have been vastly more humans than have lived to date.

·        There are extraterrestrial civilizations, in which case the no-outsider requirement is not satisfied (more on this in the next chapter). Since we wouldn’t know our absolute birth ranks on this hypothesis, DA could not be applied.

·        Leslie thinks that if the world is indeterministic, then DA is seriously weakened. (I disagree with this but list the suggestion for the sake of completeness.)

·        There are infinitely many observers in total, in which case it is not clear what DA says. (In some sense, each observer would be "infinitely early" if there were a countable number of observers.)

If one thought that DA is correct but also thought that one or more of these points represent realistic possibilities, that would not mean that DA were unimportant. Rather, it would mean that the correct conclusion would be a disjunction of possibilities rather than simply "Doom is likely to strike soon.". Such a disjunction could be both philosophically and practically interesting.

            So bearing in mind that we are regarding DA here as the general form of reasoning described above, but not necessarily leading to the prediction that doomsday will likely strike soon, let us consider some objections that have been raised against it in the literature.

CHAPTER 6: SOME ATTEMPTED REFUTATIONS OF THE DOOMSDAY ARGUMENT[49]

A vast number of objections have been fielded against DA – many of them mutually incompatible.[50] Rather than striving for completeness, we shall take aim at and refute in some detail five recent objections by Kevin Korb and Jonathan Oliver (Korb and Oliver 1999), and one other objection based on what we have called the Self-Indication Assumption. While these objections are unsuccessful, they do in some instances force us to become clearer about what DA does and doesn’t imply.[51]

Objection One

Korb and Oliver propose a minimalist constraint that any good inductive method must satisfy:

 

Targeting Truth (TT) Principle: No good inductive method should—in this world—provide no more guidance to the truth than does flipping a coin. (p. 404)

 

DA, they claim, violates this reasonable principle. In support of their claim they ask us to consider

 

a population of size 1000 (i.e., a population that died out after a total of 1000 individuals) and retrospectively apply the Argument to the population when it was of size 1, 2, 3 and so on.  Assuming that the Argument supports the conclusion that the total population is bounded by two times the sample value … then 499 inferences using the Doomsday Argument form are wrong and 501 inferences are right, which we submit is a lousy track record for an inductive inference schema. Hence, in a perfectly reasonable metainduction we should conclude that there is something very wrong with this form of inference. (p. 405)

 

But in this purported counterexample to DA, the TT principle is not violated – 501 right and 499 wrong guesses is strictly better than what one would expect from a random procedure such as flipping a coin. The reason why the track record is only marginally better than chance is simply that the above example assumes that the doomsayers bet on the most stringent hypothesis that they would be willing to bet on at even odds, i.e. that the total population is bounded by two times the sample value. This means, of course, that their expected gain is minimal. It is not remarkable, then, that in this case a person who applies the Doomsday reasoning is only slightly better off than one who doesn’t. If the bet were on the proposition not that the total population is bounded by two times the sample value but instead that it is bounded by, say, three times the sample value, then the doomsayer’s advantage would be more drastic. And the doomsayer can be even more certain that the total value will not exceed thirty times the sample value.

            Conclusion: Objection One does not show that DA violates the TT principle, nor does it show that the Doomsday reasoning at best improves the chances of being right only slightly.[52]

Objection Two

As first noted by the French mathematician Jean-Paul Delahaye in an unpublished manuscript (Delahaye 1996) of 1996, the basic Doomsday argument form can seem to be applicable not only to the survival of the human race but also to your own life span. The second of Korb and Oliver’s objections picks up on this idea:

 

[I]f you number the minutes of your life starting from the first minute you were aware of the applicability of the Argument to your life span to the last such minute and if you then attempt to estimate the number of the last minute using your current sample of, say, one minute, then according to the Doomsday Argument, you should expect to die before you finish reading this article. (fn. 2, p. 405)

 

However, this claim is incorrect. The Doomsday argument form, applied to your own life span, does not imply that you should expect to die before you have finished reading the article. DA says that in some cases you can reason as if you were a sample drawn randomly from a certain reference class. Taking into account the information conveyed by this random sample, you are to update your beliefs in accordance with Bayes’ theorem. This may cause a shift in your probability assignments in favor of hypotheses which imply that your position in the human race will have been fairly typical – say among the middle 98% rather than in the first or the last percentile of all humans that will ever have been born. DA just says you should make this Bayesian shift in your probabilities; it does not by itself determine the absolute probabilities that you end up with. As John Leslie has emphasized (e.g. Leslie 1996), what probability assignment you end up with depends on your prior, i.e. the probability assignment you started out with before taking DA into account. In the case of the survival of the human race your prior may be based on your estimates of the risk that we will be extinguished through nuclear war, germ warfare, a disaster involving future self-replicating nanomachines, a meteor impact, etc. In the case of your own life expectancy, you will want to consider factors such as the average human life span, your state of health, and any physical danger in your environment that could cause your demise before you finish the article. Based on such considerations, the probability that you will die within the next half-hour ought presumably to strike you as extremely small. But if so, then even a considerable probability shift due to a DA-like inference should not make you expect to die before finishing the article. Hence, contrary to what Korb and Oliver assert, the doomsayer would not make the absurd inference that she is likely to perish within half an hour, even would she think the Doomsday argument form applicable to her individual life span.[53]

While this is enough to refute Objection Two, the more fundamental question here is whether (and if so, how) the Doomsday argument form is applicable to individual life spans at all. I think we concede too much if we grant even a modest probability shift in this case. I have two reasons for this, which I will only outline here.

            First, Korb and Oliver’s application of the Doomsday argument form to individual life spans presupposes a specific solution to the problem of the reference class. This is the problem, remember, of determining what class of entities from which one should consider oneself a random sample. Korb and Oliver’s objection presupposes a specific solution to this problem, namely that the reference class consists of exactly those observer-moments that are aware of DA. This may not be the most plausible solution, and Korb and Oliver do not seek to justify it in any way.

            The second reason for the doomsayer not to grant a probability shift in the above example is that the no-outsider requirement is not satisfied. The no-outsider requirement states that in order for DA to be applicable in the straightforward way, there must be no outsiders – beings ignored in the reasoning that really belong inside the reference class. The issue of the no-outsider requirement holds some interest independently of its bearing on Korb and Oliver’s objection, so it is worth explaining it in some detail. John Leslie argues against the no-outsider requirement (e.g. (Leslie 1996), pp. 229–30), but I think he is mistaken for the reasons given below. (I suspect that Leslie’s thoughts on the no-outsider requirement are derived from his views on the problem of the reference class, which we found in the previous chapter to be inconsistent.)

Consider first the original application of DA (to the survival of the human species). Suppose you were certain that there is extraterrestrial intelligent life. Let’s suppose you know there are a million "small" civilizations that will have contained 200 billion persons each, and a million "large" civilizations that will have contained 200 trillion persons each. Suppose you know that the human species is one of these civilizations but you don’t know whether it is small or large.

To calculate the probability that doom will strike soon (i.e. that the human species is "Small") we can proceed in three steps:

 

Step 1. Estimate the empirical prior Pr(Small), i.e. how likely it seems that germ warfare etc. will put an end to our species before it gets large. At this stage you don’t take into account any form of the Doomsday argument or anthropic reasoning.

Step 2. Now take account of the fact that most people find themselves in large civilizations. Let H be the proposition "I am a human." And define the new probability function Pr^*( . ) = Pr( . | H) obtained by conditionalizing on H. By Bayes’ theorem,

 

.

 

A similar expression holds for ¬ Small. Assuming you can regard yourself a random sample from the set of all persons, we have

 

, and

 

.

 

(If we calculate Pr^*(Small) we find that it is very small for any realistic prior. In other words, at this stage in the calculation, it looks as if the human species is very likely long-lasting.)

Step 3. Finally we take account of DA. Let E be the proposition that you find yourself "early", i.e. that you are among the first 200 billion persons in your species. Conditionalizing on this evidence, we get the posterior probability function Pr^**( . ) = Pr^*( . | E). So

 

.

 

Note that Pr^*(E | Small) = 1 and Pr^*(E | ¬Small) = 1/1000. By substituting back into the above expressions it is then easy to verify that

 

.

 

We thus see that we get back the empirical probabilities we started from. The Doomsday argument (in Step 3) only served to cancel the effect which we took into account in Step 2, namely that you were more likely to turn out to be in the human species given that the human species is one of the large rather than one of the small civilizations. This shows that if we assume we know that there are both "large" and "small" extraterrestrial civilizations – the precise numbers in the above example don’t matter – then the right probabilities are the ones given by the naïve empirical prior.[54] Only if we there are no "outsiders" (extraterrestrial civilizations) does DA work as intended.

Returning to the case where you are supposed to apply DA to your own life span, it appears that the no-outsider requirement is not satisfied. True, if you consider the epoch of your life during which you know about DA, and you partition this epoch into time-segments (observer-moments), then you might say that if you were to survive for a long time then the present observer-moment would be extraordinary early in this class of observer-moments. You may thus be tempted to infer that you are likely to die soon (ignoring the difficulties pointed out earlier). But even if DA were applicable in this way, this would be a wrong conclusion to draw. For in this case you know for sure that there are many "outsiders". Here, the outsiders would be observer-moments of other humans. Just as the knowledge that there are large and small extraterrestrial civilizations would annul the original Doomsday argument, so in the present case does the knowledge that there are other short-lived and long-lived humans cancel the probability shift favoring impending death. The fact that the present observer-moment belongs to you would indicate that you are an individual that will have contained many observer-moments rather than few, i.e. that you will be long-lived. And it can be shown (as above) that this would counterbalance the fact that the present observer-moment would have been extraordinarily early among all your observer-moments were you to be long-lived.

Conclusion: Objection Two fails to take the prior probabilities into account. These would be extremely small for the hypothesis that you will die within the next thirty minutes. Therefore, contrary to what Korb and Oliver claim, even if the doomsayer thought DA applied to this case, he would not make the prediction that you would die within 30 minutes. However, the doomsayer should not reckon DA applicable in this case, for two reasons. First, it presupposes an arguably implausible solution to the reference class problem. Second, even if we accept that only beings who know about DA should be in the reference class, and that it is legitimate to run the argument on time-segments of observers, the conclusion will still not follow; for the no-outsider requirement is not satisfied.

Objection Three

Korb and Oliver’s third objection starts off with the claim that (in a Bayesian framework) a sample size of one is too small to make a substantial difference to one’s rational beliefs.

 

The main point … is quite simple: a sample size of one is "catastrophically" small.  That is, whatever the sample evidence in this case may be, the prior distribution over population sizes is going to dominate the computation.  The only way around this problem is to impose extreme artificial constraints on the hypothesis space. (p. 406)

 

They follow this assertion by conceding that in a case where the hypothesis space contains only two hypotheses, a substantial shift can occur:

 

If we consider the two urn case described by Bostrom, we can readily see that he is right about the probabilities. (p. 406)

 

The probability in the example they refer to shifted from 50% to 99.999%, which is surely "substantial", and a similar result would be obtained for a broad range of distributions of prior probabilities. But Korb and Oliver seem to think that such a substantial shift can only occur if we "impose extreme artificial constraints on the hypothesis space" by considering only two rival hypotheses rather than many more.

            It is easy to see that this is false. Let {h₁, h₂, …h_N} be an hypothesis space and let P be any probability function that assigns a non-zero prior probability to all these hypotheses. Let h_i be the least likely of these hypotheses. Let e be the outcome of a single random sampling. Then it is easy to see, just by inspecting Bayes’ formula, that the posterior probability of h_i, P(h_i | e), can be made arbitrarily big () by an appropriate choice of e:

 

.

 

Choosing e such that P(e|h_j) is small for , we have

 

.

 

Indeed, we get P(h_i|e) = 1 if we choose e such that P(e|h_j) = 0 for . This would for example correspond to the case where you discover that you have a birth rank of 200 billion and immediately give probability zero to all hypotheses according to which there would be less than 200 billion persons.

Conclusion: Korb and Oliver are wrong when they claim that the prior distribution is always going to dominate over any computation based on a sample size of one.

Objection Four

By increasing the number of hypotheses about the ultimate size of the human species that we choose to consider, we can, according to Korb and Oliver, make the probability shift that DA induces arbitrarily small[55]:

 

In any case, if an expected population size for homo sapiens … seems uncomfortably small, we can push the size up, and so the date of our collective extermination back, to an arbitrary degree simply by considering larger hypothesis spaces. (p. 408)

 

The argument is that if we use a uniform prior over the chosen hypothesis space {h₁, h₂, ..., h_n}, where h_i is the hypothesis that there will have existed a total of i humans, then the expected number of humans that will have lived will depend on n: the greater the value we give to n, the greater the expected future population. Korb and Oliver compute the expected size of the human population for some different values of n and find that the result does indeed vary.

            Notice first of all that nowhere in this is there a reference to DA. If this argument were right it would work equally against any way of making predictions about how long the human species will survive. For example, if during the Cuba missile crisis you feared – based on obvious empirical factors – that humankind might soon go extinct, you really needn’t have worried. You could just have considered a larger hypothesis space and you would thereby have reached an arbitrarily high degree of confidence that doom was not impending. If only making the world safer were that easy.

            What, then, is the right prior to use for DA? All we can say about this from a general philosophical point of view is that it is the same as the prior for people who don’t believe in DA. The doomsayer does not face a special problem here. The only legitimate way of providing the prior is through an empirical assessment of the potential threats to human survival. You need to base it on your best guesstimates about the hazards of germ warfare, nuclear warfare, weapons based on nanotechnology, asteroids or meteors striking the Earth, a runaway greenhouse effect, future high-energy physics experiments, and other dangers as yet unimagined.[56]

            On a charitable reading, Korb and Oliver could perhaps be interpreted as saying not that DA fails because the prior is arbitrary, but rather that the uniform prior (with some big but finite cut-off point) is as reasonable as any other prior, and that with such a prior DA will not show that doom is likely to strike very soon. If this is all they mean then they are not saying something that the doomsayer could not agree with. The doomsayer (i.e. a person who believes DA is sound) is not committed to the view that doom is likely to strike soon[57], only to the view that the risk that doom will strike soon is greater than was thought before we understood the probabilistic implications of our having relatively low birth ranks. DA (if sound) shows that we have systematically underestimated the risk of doom soon, but it doesn’t directly imply anything about the absolute magnitude of the probability of that hypothesis. (For example, John Leslie, who strongly believes in DA, still thinks there is a 70% chance that we will colonize the galaxy.) Even with a uniform prior probability, there will still be a shift in our probability function in favor of earlier doom.

            But don’t Korb and Oliver’s calculations at least show that this probability shift in favor of earlier doom is in reality quite small, so that DA isn’t such a big deal after all? No, their calculations do not show that, for two reasons.

The first reason is that as already mentioned, their calculations rest on the assumption of a uniform prior. Not only is this assumption gratuitous – no attempt is made to justify it – but it is also, I believe, highly implausible even as an approximation of the real empirical prior. Personally I think it is fairly obvious that given what I know (and before considering DA), the probability that there will exist between 100 billion and 500 billion humans is much greater than the probability that there will exist between 10²⁰ and (10²⁰ + 500 billion) humans.

Second, even granting the uniform prior, it turns out that the probability shift is actually quite big. Korb and Oliver assume a uniform distribution over the hypothesis space {h₁, h₂, …, h_2,048} (where again h_i is the hypothesis that there will have been a total of i billion humans) and they assume that you are the 60 billionth human. Then the expected size of the human population before considering DA is  994 billion. And Korb and Oliver’s calculations show that after applying DA the expected population is 562 billion. The expected human population has been reduced by over 43% in their own example.

            Conclusion: Objection Four fails. Korb and Oliver’s argument about being able to get an arbitrarily large expected population by assuming a uniform prior and making the hypothesis space sufficiently big is misguided; if correct, this objection would work equally well against predictions that do not use DA. For the doomsayer and the non-doomsayer use the same prior probability, the one determined by ordinary empirical considerations. Moreover, the doomsayer is not committed to the view that doom will likely strike soon, only that the risk has been systematically underestimated. Korb and Oliver have not showed that the risk has been only slightly underestimated. On the contrary, in Korb and Oliver’s own example DA cuts the expected population by nearly one half.

Objection Five

Towards the end of their paper, Korb and Oliver hint at a fifth objection: that we shouldn’t regard ourselves as random samples from the human species (or the human species cum its intelligent robot descendants) because there is a systematic correlation between our genetic makeup and our personal identity:

 

… the notion that anyone is uniformly randomly selected from among the total population of the species is beyond far fetched. The bodies that we are, or supervene upon, have a nearly fixed position in the evolutionary order; for example, given what we know of evolution it is silly to suppose that someone’s DNA could precede that of her or his ancestors. (p. 408)

 

The doomsayer will grant all this. But even if the exact birth order of all humans could be inferred from a list of their genomes, the only thing that would show is that there is more than one way of finding out about somebody’s birth rank. In addition to the usual way – observing what year it is and combining that information with our knowledge of past population figures –there would now be an additional method of obtaining the same number: by analyzing somebody’s DNA and consulting a table correlating DNA with birth rank.

            The same holds for other correlations that may obtain. For example, the fact that I am wearing contact lenses indicates that I am living after the year 1900 A.D. This gives me a way of estimating my birth rank—check whether I have contact lenses and, if so, draw the conclusion that it is past the year 1900 A.D. Comparing this with past population figures then tells me something about my birth rank. But none of these correlations add anything new once you have found at least one way of determining your birth rank.

            Conclusion: It is true that there is a systematic correlation between one’s genetic makeup and one’s birth rank. The presence of such a correlation gives us an alternative (though impractical) way of ascertaining one’s birth rank but it does not affect the evidential relation between having this birth rank and any general hypothesis about humankind’s future. That you can indeed legitimately regard yourself as in some sense randomly selected from a group of people even in cases where these people have different genes can be argued for in various ways, as we saw in chapter 4. (Unfortunately, Korb and Oliver do not attempt to criticize or discuss any of the arguments for the randomness assumption). Thus, the fifth objection fails to refute DA.

The Self-Indication Assumption

We now turn to an objection that is not made by Korb and Oliver but which can be spotted lurking in the background of many other attacks on DA. This objection is based on the Self-Indication Assumption (SIA), which we encountered briefly in chapter 4. Framed as an attack on DA, the idea is that the probability shift in favor of Doom Soon that DA leads us to make is offset by another probability shift – which is overlooked by DA proponents – in favor of Doom Late. When both these probability shifts are taken into account, the net effect is that we end up with the naïve probability estimates that we made before we learnt about either DA or SIA. According to this objection, the more observers that will ever have existed, the more "slots" would there be that you could have been "born into". Your existence is more probable if there are many observers than if there are few. Since you do in fact exist, the Bayesian rule has to be applied and the posterior probability of hypotheses which imply that many observers exist must be increased accordingly. The nifty thing is that the effects of SIA and DA cancel each other precisely, as can be seen through a trivial calculation[58]:

 

Let  be the naive prior for the hypothesis that in total i observers will have existed, and assume that  for i greater than some finite N. (This restriction allows us to set aside the problem of infinities.) Then we can formalize SIA as saying that

 

 

where  is a normalization constant. Let r(x) be the rank of x, and let "I" denote a random sample from a uniform probability distribution over the set of all observers. By SSA, we have

 

 

Consider two hypotheses h_n and h_m. We can assume that . (If not, then the example simplifies to the trivial case where one of the hypotheses is conclusively refuted regardless of whether SIA is accepted.) Using Bayes’ formula, we expand the quotient between these two hypotheses:

 

.

 

We see that after we have applied both SIA and DA, we are back to the naive probabilities that we started with.

 

            Why accept SIA? The fact that SIA has the virtue of leading to a complete cancellation of DA may well be the most positive thing that can be said on its behalf. As an objection against DA, this argument would be unabashedly question-begging. It could still carry some weight if DA were sufficiently unacceptable and if there were no other coherent way of avoiding its conclusion. However, that is not the case. We shall examine another coherent way of resisting DA in chapter 9. Even if the choice were between SIA and the DA-conclusion, I would still lean towards the latter alternative as the lesser of two evils.

            We saw in chapter 2 why, owing to observational selection effects, it would be a mistake to use the fine-tuning of our universe as an argument for hypotheses that imply a greater number of observer-containing universes. If two competing general hypotheses each imply that there is at least one observer-containing universe, but one of the hypotheses implies a greater number of observer-containing universes than the other, then fine-tuning is not typically a reason to favor the former. This reasoning can be adapted to argue that your own existence is not in general a ground for thinking that hypotheses are more likely to be true if they imply a greater total number of observers in existence. The datum of your existence tends to disconfirm hypotheses on which it would be unlikely that even a single observer should exist, but that’s as far as it goes.[59] And the reason for this is that the sample at hand – yourself – should not be regarded as randomly selected from the class of all possible observers but only from the class of observers that will actually have existed. It is, so to speak, not a coincidence that the sample you are considering is one which actually exists; rather, that’s a logical consequence from the fact that only actual observers actually view themselves as samples from anything at all.

            Further reasons for rejecting SIA are generated when we consider what accepting it would entail that we should believe in circumstances where we are ignorant of our birth ranks so that the counterbalancing probability shift due to DA does not take place. In these cases, SIA entails a uniform a priori bias in favor of worlds with many observers. It is easy to see that in order for SIA always to be able to cancel DA, you would have to subscribe to the principle that, other things equal, a hypothesis which implies that there are 2N observers should be assigned twice the credence of a hypothesis which implies that there are only N observers. In the case of the God’s Coin Toss gedanken, this means that before learning about the color of your beard, you should think it likely that the coin fell heads (so that two observers rather than just one were created). If we modify the gedanken so that heads would lead to the creation of a million observers, you would have to be virtually certain – before knowing anything directly about the outcomes and before learning about your beard-color – that the coin fell heads, even if you knew that it had a ten thousand to one bias in favor of tails. This seems wrong.

            Nor is it only in fictional toy examples, which we know will not actually obtain, that we would get counterintuitive results from accepting SIA. For as a matter fact, we may well be radically ignorant of our birth ranks (namely if there are extraterrestrial species). Consider the following gedanken:

 

The presumptuous philosopher

It is the year 2100 and physicists have narrowed down the search for a theory of everything to only two remaining plausible candidate theories, T1 and T2 (using considerations from super-duper symmetry). According to T1 the world is very, very big but finite, and there are a total of a trillion trillion observers in the cosmos. According to T2, the world is very, very, very big but finite, and there are a trillion trillion trillion observers. The super-duper symmetry considerations seem to be roughly indifferent between these two theories. The physicists are planning on carrying out a simple experiment that will falsify one of the theories. Enter the presumptuous philosopher: "Hey guys, it is completely unnecessary for you to do the experiment, because I can already show to you that T2 is about a trillion times more likely to be true than T1 (whereupon the philosopher runs the God’s Coin Toss thought experiment and explains Model 3)!"

 

One suspects the Nobel Prize committee to be a bit hesitant about awarding the presumptuous philosopher the big one for this contribution.

 

CHAPTER 7: OBSERVER-RELATIVE CHANCES IN ANTHROPIC REASONING?[60]

This chapter examines an argument by John Leslie (Leslie 1997) purporting to show that anthropic reasoning gives rise to paradoxical "observer-relative chances" [61]. I show that the argument trades on the sense/reference ambiguity and is fallacious. I then describe a related case where chances are observer-relative in an interesting way. But not in a paradoxical way. The result can be generalized: At least for a very wide range of cases, SSA does not engender paradoxical observer-relative chances.

Leslie’s argument and why it fails

The conclusion that Leslie seeks to establish is that:

 

Estimated probabilities can be observer-relative in a somewhat disconcerting way: a way not depending on the fact that, obviously, various observers often are unaware of truths which other observers know. (p. 435)

 

Leslie does not regard this as a reductio of anthropic reasoning but rather suggests bullet-biting as the correct response: "Any air of paradox must not prevent us from accepting these things." (p. 428).

Leslie’s argument takes the form of a gedanken. Suppose we start with a batch of one hundred women and divide them randomly into two groups, one with ninety-five and one with five women. By flipping a fair coin, we then assign the name ‘the Heads group’ randomly to one of these groups and the name ‘the Tails group’ to the other. According to Leslie it is now the case that an external observer, i.e. a person not in either of the two groups, ought to derive radically different conclusions than an insider:

 

All these persons – the women in the Heads group, those in the Tails group, and the external observer – are fully aware that there are two groups, and that each woman has a ninety-five per cent chance of having entered the larger. Yet the conclusions they ought to derive differ radically. The external observer ought to conclude that the probability is fifty per cent that the Heads group is the larger of the two. Any woman actually in [either the Heads or the Tails group], however, ought to judge the odds ninety-five to five that her group, identified as ‘the group I am in’, is the larger, regardless of whether she has been informed of its name. (p. 428)

 

Even without knowing her group’s name, a woman could still appreciate that the external observer estimated its chance of being the larger one as only fifty per cent – this being what his evidence led him to estimate in the cases of both groups. The paradox is that she herself would then have to say: ‘In view of my evidence of being in one of the groups, ninety-five per cent is what I estimate.’ (p. 429)

 

Somewhere within these two paragraphs a mistake has been made. It’s not hard to locate the error if we look at the structure of the reasoning. Let’s say there is a woman in the larger group who is called Chris. The "paradox" then takes the following form:

 

(1) Pr_Chris ("The group that Chris is in is the larger group") = 95%

 

(2) The group that Chris is in = the Heads group

 

(3) Therefore: Pr_Chris ("The Heads group is the larger group") = 95%

 

(4) But Pr_{External observer} ("The Heads group is the larger group") = 50%

 

(5) Hence chances are observer-relative.

 

Where it goes wrong is in step (3). The group that Chris is in is indeed identical to the Heads group, but Chris doesn’t know that. Pr_Chris ("The Heads group is the larger group") = 50%, not 95% as claimed in step (3). There is nothing paradoxical or surprising about this, at least not any longer after Frege’s discussion of Hesperus and Phosphorus. One need not have rational grounds for assigning probability one to the proposition "Hesperus = Phosphorus", even though as a matter of fact Hesperus = Phosphorus. For one might not know that Hesperus = Phosphorus. The expressions ‘Hesperus’ and ‘Phosphorus’ present their denotata under different modes of presentation: they denote the same object while connoting different concepts. There is disagreement over exactly how to describe this difference and what general lesson to learn from it; but the basic observation that you can learn something from being told "a = b" (even if a = b) is neither new nor has it very much in particular to do with SSA.

Let’s see if there is some way we could rescue Leslie’s conclusion by modifying the thought experiment.

Suppose that we change the example so that Chris now knows that the sentence "Chris is in the Heads group" is true. Then step (3) will be correct. However, we will now run into trouble when we try to take step (5). It will no longer be true that Chris and the external observer know about the same facts. Chris’s information set now contains the sentence "Chris is in the Heads group". The external observer’s information set doesn’t contain this piece of information. So no interesting form of observer-relative chances has been established.

            What if we change the example again and assume that the external observer, too, knows that Chris is in the Heads group? Well, if Chris and the external observer agreed on the chance that the Heads group is the large group before they both learnt that Chris is in the Heads group, then they will continue to be in agreement about this chance after they have received that information – provided they agree about the conditional probability Pr (The Heads group is the larger group | Chris is in the Heads group.). This, then, is what we have to examine to see if any paradoxical conclusion can be wrung from Leslie’s set-up: we have to check whether Chris and the outside observer agree on this conditional probability.

            First look at it from Chris’ point of view. Let’s go along with Leslie and assume that she should think of herself as a random sample from the batch of one hundred women. Suppose she knows that her name is Chris (and that she’s the only woman in the batch with that name). Then, before she learns that she is in the Heads group, she should think that the probability of that being the case is 50%. (Recall that what group should be called ‘the Heads group’ was determined by tossing of a fair coin.) She should think that the chance of the sentence "Chris is in the larger group" is 95%, since ninety-five out of the hundred women are in the larger group, and she can regard herself as a random sample from these hundred women. When learning that she is in the Heads group, the chance of her being in the larger group remains 95%. (‘the Heads group’ and ‘the Tails group’ are just arbitrary labels at this point; randomly calling one group the Heads group doesn’t change the likelihood that it is the big group.) Hence the probability she should give to the sentence "The Heads group is the larger group" is now 95%. Therefore the conditional probability which we were looking for is Pr_Chris ("The Heads group is the larger group" | "Chris is in the Heads group") = 95%.

            Next consider the situation from the external observer’s point of view. What is the probability for the external observer that the Heads group is larger given that Chris is in it? Well, what’s the probability that Chris is in the Heads group? In order to answer these questions, we need to know something about how this woman Chris was selected.

Suppose that she was selected as a random sample (with uniform sampling density) from among all the hundred women in the batch. Then the external observer would arrive at the same conclusion as Chris: if the random sample ‘Chris’ is in the Heads group then there is a 95% chance that the Heads group is the bigger group.

If we instead suppose that Chris was selected randomly from some subset of the hundred women, then it might happen that the external observer’s estimate diverges from Chris’. For example, if the external observer randomly selects one individual x (whose name happens to be ‘Chris’) from the large group, then, when he finds that x is in the Heads group, he should assign a 100% probability to the sentence "The Heads group is the larger group." This is indeed a different conclusion than the one which the insider Chris draws. She thought the conditional probability of the Heads group being the larger given that Chris is in the Heads group was 95%.

            In this case, however, we have to question whether Chris and the external observer know about the same evidence. (If they don’t, then the disparity in their conclusions doesn’t signify that chances are observer-relative in any paradoxical sense.) But it is clear that their information sets do differ in a relevant way. For suppose Chris got to know what the external observer is stipulated to already know: that Chris had been selected by the external observer through some random sampling process from among a certain subset of the hundred women. That implies that Chris is a member of that subset. This information would change her probability estimate so that it once again becomes identical to the external observer’s. In the above case, for instance, the external observer selected a woman randomly from the large group. Now, evidently, if Chris gets this extra piece of information, that she has been selected as a random sample from the large group, then she knows with certainty that she is in that group; so her conditional probability that the Heads group is the larger group given that Chris is in the Heads group should then be 100%, the same as what the outside observer should believe.

We see that as soon as we give the two people access to the same evidence, their disagreement vanishes. There are no paradoxical observer-relative chances in this thought experiment.[62]

Observer-relative chances: another try

In this section I shall give an example where chances could actually be said to be observer-relative in an interesting – though by no means paradoxical – sense. What philosophical lessons we should or shouldn’t learn from this phenomenon will be discussed in the next section.

Here is the example:

 

Suppose the following takes place in an otherwise empty world. A fair coin is flipped by an automaton and if it falls heads, ten humans are created; if it falls tails, one human is created. Suppose that in addition to these people there is one additional human that is created independently of how the coin falls. This latter human we call the bookie. The people created as a result of the coin toss we call the group. Everybody knows these facts. Furthermore, the bookie knows that she is the bookie and the people in the group know that they are in the group.

 

            The question is what are the fair odds if the people in the group want to bet against the bookie on how the coin fell? One could think that everybody should agree that the chance of it having fallen heads is fifty-fifty, since it was a fair coin. That overlooks the fact that the bookie obtains information from finding that she is the bookie rather than one of the people in the group. This information is relevant to her estimate of how the coin fell. It is more likely that she should find herself being the bookie if one out of two is a bookie than if the ratio is one out of eleven. So finding herself being the bookie, she obtains reason to believe that the coin probably fell tails, leading to the creation of only one other human. In a similar way, the people in the group, by observing that they are in the group, obtain some evidence that the coin fell heads, resulting in a large fraction of all observers observing that they are in the group.

            It is a simple exercise to use Bayes’ theorem to calculate what the posterior probabilities are after this information has been taken into account.

 

Since the coin is fair, we have Pr (Heads) = Pr (Tails) = ½.

 

By SSA, Pr (I am bookie | Heads) = and Pr (I am bookie | Tails) = ½. Hence,

 

Pr (I am bookie)

= Pr (I am bookie | Heads) ∙ Pr (Heads) + Pr (I am bookie | Tails) ∙ Pr (Tails)

=  ∙  ½ + ½ ∙  ½ = .

 

From Bayes’ theorem we then get:

 

Pr (Heads | I am bookie)

= Pr (I am bookie | Heads) ∙ Pr (Heads) / Pr (I am bookie)

                        =  = .

 

In exactly the same way we get the odds for the people in the group:

 

Pr (I am in the group | Heads) =

Pr (I am in the group | Tails) = ½.

Pr (I am in the group) =  ∙  ½ + ½ ∙  ½ = .

Pr (Heads | I am in the group) = Pr (I am in the group | Heads) ∙ Pr (Heads) / Pr (I am in the group)

=  = .

 

We see that the bookie should think there is a  chance that the coin was heads while the people in the group should think that the chance is . This is a consequence of SSA.

Discussion

While it might be slightly noteworthy that the bookie and the people in the group are rationally required to disagree in the above scenario, it isn’t the least bit paradoxical. Their information sets are not identical. For instance, the bookie knows that "I am the bookie.". That is clearly a different proposition from the corresponding one – "I am in the group." – known by the people in the group. So chances have not been shown to be observer-relative in the sense that people with the same information can be rationally required to disagree. And if we were to try to modify the example so as to make the participants’ information sets identical, we would see that their disagreement disappears; as it did when we attempted various twists of the Leslie gedanken.

            There is a sense, though, in which the chances in the present example can be said to be observer-relative. The information sets of the bookie and the people in the group, while not identical, are quite similar. They differ only in regard to such indexical facts[63] as "I am the bookie." or "I am in the group.". We could say that the example demonstrates, in an interesting way, that chances can be relative to observers in the sense that: people with information sets that are identical up to indexical facts can be rationally required to disagree about non-indexical facts.

            This kind of observer-relativity is not particularly counterintuitive and it should not be taken to cast doubt on SSA from which it was derived. That indexical facts can have implications for what we should believe about nonindexical facts shouldn’t surprise us. It can be shown by a very simple example: from "I have steel-blue eyes." it follows that somebody has steel-blue eyes.

            The rational odds in the example above being different for the bookie than for the punters in the group, we might begin to wonder whether it is possible to formulate some kind of bet for which all parties would calculate a positive expected payoff? This would not necessarily be an unacceptable consequence since the bettors have different information. Still, it could seem a bit peculiar if we had a situation where purely by applying SSA rational people were led to start placing bets against one another.

            So it is worth calculating the odds to see if there are cases where they do indeed favour betting. This is done in an appendix. The result turns out to be negative – no betting. In the quite general class of cases considered, there is no combination of parameter values for which a bet is possible in which both parties would rationally expect a positive non-zero payoff.[64]

            This result is reassuring for the anthropic theorizer. Yet we are still left with the fact that there are cases where observers come to disagree with each other just because of applying SSA. While it is true that these disagreeing observers will have different indexical information, and while there are trivial examples in which a difference in indexical information implies a difference in non-indexical information, it might nonetheless be seen as objectionable that anthropic reasoning should lead to this kind of disagreements. Does not that require that we ascribe some mysterious quality to the things we call "observers", some property of an observer’s mind that cannot be reduced to objective observer-independent facts?

The best way to resolve this scruple is to show how the above example, where the "observer-relative" chances appeared, can be restated in purely physicalistic terms:

 

A coin is tossed and either one or ten human brains are created. These brains make up ‘the group’. Apart from these there is only one other brain, the ‘bookie’. All the brains are informed about the procedure that has taken place. Suppose Alpha is one of the brains that have been created and that Alpha remembers recently having been in the brain states A₁, A₂, ..., A_n. (I.e. Alpha recognizes the descriptions "A₁", "A₂", ..., "A_n" descriptions of these states, and Alpha knows "this brain was recently in states A₁, A₂, ..., A_n" is true. Cf. Perry (1979).)

At this stage, Alpha should obviously think the probability that the coin fell heads is 50%, since it was a fair coin. But now suppose that Alpha is informed that he is the bookie, i.e. that the brain that has recently been in the states A₁, A₂, ..., A_n is the brain that is labeled ‘the bookie’. Then Alpha will reason as follows:

"Let A be the brain that was recently in states A₁, A₂, ..., A_n. The conditional probability that A is labeled ‘the bookie’ given that A is one of two existing brains is greater than the conditional probability that A is the brain labeled ‘the bookie’ given that A is one out of eleven brains. Hence, since A does indeed turn out to be the brain labeled ‘the bookie’, there is a greater than 50% chance that the coin fell tails, creating only one brain."

 

A parallel line of reasoning can be pursued by a brain labeled ‘a brain in the group’. The argument can be quantified in the same way as in the earlier example and will result in the same "observer-relative" chances. This shows that anthropic reasoning can be understood in a purely physicalistic framework.

The observer-relative chances in this example too are explained by the fact that the brains have access to different evidence. Alpha, for example, knows that (P_Alpha:) the brain that has recently been in the states A₁, A₂, ..., A_n is the brain that is labeled ‘the bookie’. A brain, Beta, who comes to disagree with Alpha about the probability of heads, will have a different information set. Beta might for instance rather know that (P_Beta:) the brain that has recently been in the states B₁, B₂, ..., B_n is a brain that is labeled ‘a member of the group’. P_Alpha is clearly not equivalent to P_Beta.

            It is instructive to see what happens if we take a step further and eliminates from the example not only all non-physicalistic terms but also its ingredient of indexicality:

 

In the previous example we assumed that the proposition (P_Alpha) which Alpha knows but Beta does not know was a proposition concerning the brain states A₁, A₂, ..., A_n of Alpha itself. Suppose now instead that Alpha does not know what label the brain Alpha has (whether it is ‘the bookie’ or ‘a brain in the group’) but that Alpha has been informed that there are some recent brain states G₁, G₂, ..., G_n of some other existing brain, Gamma, and that Gamma is labeled ‘the bookie’.

 

At this stage, what conclusion Alpha should draw from this piece of information is underdetermined by the specifications we have given. It would depend on what Alpha would know or guess about how this other brain Gamma had been selected to come to Alpha’s notice. Suppose we specify the thought experiment further by stipulating that, as far as Alpha’s knowledge goes, Gamma can be regarded as a random sample from the set of all existing brains. Alpha may know, say, that one ball for each existing brain was put in an urn and that one of these balls was drawn at random and it turned out to be the one corresponding to Gamma. Reasoning from this information, Alpha will arrive at the same conclusion as if Alpha had learnt that Alpha was labeled ‘the bookie’ as was the case in the previous version of the thought experiment. Similarly, Beta may know about another random sample, Epsilon, that is labeled ‘a brain in the group’. This will lead Alpha and Beta to differ in their probability estimates, just as before. In this version of the thought experiment no indexical evidence is involved. Yet Alpha’s probabilities differ from Beta’s.

 

What we have here is hardly distinct from any humdrum situation where John and Mary know different things and therefore estimate probabilities differently. The only difference between the present example and a commonplace urn game is that here we are dealing in brains whereas there we are dealing in raffle tickets – surely not philosophically relevant.

But what exactly did change when we removed the indexical element? If we compare the two last examples we see that the essential disparity is in how the random samples were produced.

In the second of the two examples there was a physical selection mechanism that generated the randomness. We said that Alpha knew that there was one ball for each brain in existence, that these balls had been put in an urn, and that one of these balls had then been selected randomly and had turned out to correspond to a brain that was labeled ‘the bookie’.

In the other example, by contrast, there was no such physical mechanism. Instead, there the randomness did somehow arise from each observer considering herself as a random sample from the set of all observers. Alpha and Beta observed their own states of mind (i.e. their own brain states). Combining this information with other, non-indexical, information allowed them to draw conclusions about non-indexical states of affairs that they could not draw without the indexical information obtained from observing their own states of mind. But there was no physical randomization mechanism at work analogous to selecting a ball from an urn.

Now, it is may indeed be problematic how such reasoning can be justified or explained – that is after all the subject matter of this dissertation. However, SSA is precisely what is used to get anthropic reasoning off the ground in the first place. So the discovery that SSA leads to "observer-relative" chances, and that these chances arise without an identifiable randomization mechanism, is not something that should add new scruples. It merely amounts to a restatement of the assumption from which we started.

Conclusion

Leslie’s argument that there are cases where anthropic reasoning gives rise to paradoxical observer-relative chances does not hold up to scrutiny. We argued that it rests on a sense/reference ambiguity and that when this ambiguity is resolved then the purported observer-relativity disappears. Several ways in which one could try to salvage Leslie’s conclusion were explored and it turned out that none of them would work.

            We then considered an example where observers applying SSA end up disagreeing about the outcome of a coin toss. The observers’ disagreement depends on a difference in their information sets and is not of a paradoxical nature; there are completely trivial examples of the same kind of phenomenon. We also showed that (at least for a wide range of cases) this disparity in beliefs cannot be marshaled into a betting arrangement where all parties involved would expect to make a gain.

This example was given a physicalistic reformulation showing that the observers’ disagreement does not imply some mysterious irreducible role for the observers’ consciousness. What does need to be presupposed, however, unless the situation be utterly trivialized, is SSA. This is not a finding that should be taken to cast doubt on anthropic reasoning. Rather, it simply elucidates one aspect of what SSA really means. The absence the sort of paradoxical observer-relative chances that Leslie claimed to have found could even be taken to give some indirect support for SSA.

Appendix

In this appendix it is shown for a quite general set of cases that adopting and applying SSA does not lead rational agents to bet against one another.

            Consider again the case where a fair coin is tossed and a different number of observers are created depending on how the coin falls. The people created as a result of the coin toss make up ‘the group’. In addition to these there exists a set of people we call the ‘bookies’. Together, the people in the group and the bookies make up the set of people who are said to be ‘in the experiment’. To make the example more general, we also allow there to be (a possibly empty) set of observers who are not in the experiment (i.e. who are not bookies and are not in the group); we call these observers ‘outsiders’.

We introduce the following abbreviations:

 

Number of people in the group if coin falls heads = h

Number of people in the group if coin falls tails = t

Number of bookies = b

Number of outsiders = u

For "The coin fell heads.", write H

For "The coin fell tails.", write ¬H

For "I am in the group.", write G

For "I am a bookie.", write B

For "I am in the experiment (i.e. I’m either a bookie or in the group)", write E

 

First we want to calculate Pr(H|G&E) and Pr(H|B&E), the probabilities that the groupies and the bookies, respectively, should assign to the proposition that the coin fell heads. Since G implies E, and B implies E, we have Pr(H|G&E) = Pr(H|G) and Pr(H|B&E) = Pr(H|B). We can derive Pr(H|G) from the following equations:

 

Pr(H|G) = Pr(G|H) Pr(H) / Pr(G)                     (Bayes’ theorem)

Pr(G|H) = h / (h + b + u)                                 (SSA)

Pr(G|¬H) = t / (t + b + u)                                (SSA)

Pr(H) = Pr(¬H) = ½                                        (Fair coin)

Pr(G) = Pr(G|H) Pr(H) + Pr(G|¬H) Pr(¬H)     (Theorem)

 

This gives us

 

Pr(H|G&E) = .

 

In an analogous fashion, using Pr(B|H) = b / (h + b + u) and Pr(B|¬H) = b / ( t + b + u), we get

 

Pr(H|B&E) = .

 

We see that Pr(H|B&E) is not in general equal to Pr(H|G&E). The bookies and the people in the group will arrive at different estimates of the probability that the coin was heads. For instance, if we have the parameter values {h = 10, t = 1, b = 1, u = 10} we get Pr(H|G&E)  85% and Pr(H|B&E)  36%. In the limiting case when the number of outsiders is zero, {h = 10, t = 1, b = 1, u = 0}, we have Pr(H|G&E)  65% and Pr(H|B&E)  15% (which coincides with the result in section 3). In the opposite limiting case, when the number of outsiders is large, {h = 10, t = 1, b = 1, }, we get Pr(H|G&E)  91% and Pr(H|B&E) = 50%. In general, we should expect the bookies and the groupies to disagree about the outcome of the coin toss.

Now that we know the probabilities can check whether a bet occurs. There are two types of bet that we will consider. In a type1 bet a bookie bets against the group as a whole, and the group members bet against the set of bookies as a whole. In a type 2 bet an individual bookie bets against an individual group member.

Let’s look at the type 1 bet first. The maximal amount $x that a person in the group is willing to pay to each bookie if the coin fell heads in order to get $1 from each bookie if it was tails is given by

 

Pr(H|G)(–x)b + Pr(¬H|G)b = 0.

 

When calculating the rational odds for a bookie we have to take into account the fact that depending on the outcome of the coin toss, the bookie will turn out to have betted against a greater or smaller number of group members. Keeping this in mind, we can write down a condition for the minimum amount $y that a bookie has to receive (from every group member) if the coin fell heads in order to be willing to pay $1 (to every group member) if it fell tails:

 

Pr(H|B) y ∙ h + Pr(¬H|B)(–1)t = 0.

 

Solving these two fairness equations we find that x = y = , which means that nobody expects to win from a bet of this kind.

            Turning now to the type 2 bet, where individual bookies and individuals in the group bet directly against each other, we have to take into account an additional factor. To simplify things, we assume that it is assured that all of the bookies get to make a type 2 bet and that no person in the group bets against more than one bookie. This implies that the number of bookies isn’t greater than the smallest number of group members that could have resulted from the coin toss; for otherwise there would be no guarantee that all bookies could bet against a unique group member. But this means that if the coin toss generated more than the smallest possible number of group members then a selection has to be made as to which of the group members get to bet against a bookie. Consequently, a group member who finds that she has been selected obtains reason for thinking that the coin fell in such a way as to maximize the proportion of group members that get selected to bet against a bookie. (The bookies’ probabilities remain the same as in the previous example.)

            Let’s say that it is the tails outcome that produces the smallest group. Let s denote the number of group members that are selected. We require that . We want to calculate the probability for the selected people in the group that the coin was heads, i.e. Pr(H|G&E&S). Since S implies both G and E, we have Pr(H|G&E&S) = Pr(H|S). Using

 

Pr(H|S) = Pr(S|H) Pr(H) / Pr(S)                        (Bayes’ theorem)

Pr(S|H) = s / (h + b + u)                                   (SSA)

Pr(S|¬H) = s / (t + b + u)                                 (SSA)

Pr(H) = Pr(¬H) = 1/2                                      (Fair coin)

Pr(S) = Pr(S|H)Pr(H) + Pr(S|¬H)Pr(¬H)          (Theorem)

 

we get

 

Pr(H|G&E&S) = .

 

Comparing this to the result in the previous example, we see that Pr(H|G&E&S) = Pr(H|B&E). This means that the bookies and the group members that are selected now agree about the odds. So there is no possible bet between them for which both parties would calculate a positive non-zero expected payoff.

            We conclude that adopting SSA does not lead observers to place bets against each other. Whatever the number of outsiders, bookies, group members and selected group members, there are no bets, either of type 1 or of type 2, from which all parties should expect to gain.

CHAPTER 8: PARADOXES OF THE SELF-SAMPLING ASSUMPTION[65]

While chapter 7 sent a rather reassuring message about SSA, this chapter exposes some problematic consequences that seem to flow from SSA. These are uncovered with the help of four thought experiments. Among the prima facie results are that SSA implies that it is reasonable to believe in backward causation and paranormal causation, such as psychokinesis, and that SSA recommends actions that seem radically foolish. The rest of the chapter attempts to determine which if any of these prima facie implications are genuine, and if so, to assess how strongly they count against SSA. To anticipate the outcome, it will be shown that none of the most paradoxical implications obtain. However, some counterintuitive consequences are genuine. They could be taken as reasons for rejecting or modifying SSA. In the next chapter we will consider this option further.

Four gedanken wherein SSA yields counterintuitive results

The thought experiments we shall conduct here all variations on the same theme. They put different problematic aspects of SSA into focus.

 

Experiment #1: What the snake said to Eve

Eve and Adam, the first two persons, knew that if they had sex Eve might have a child, and if she did, they would be driven out from Eden and would go on to have billions of progeny that would fill the Earth with misery. One day a snake sneaked up to Eve and said to her: "Pssst, listen! If you have sex with Adam, then either you will have a child or you won’t. If you have child then you will have been among the first two out of billions of people. You would have had an extraordinarily early position in the human race. If, one the other hand, you don’t become pregnant then you and Adam will turn out to have very typical positions. By Bayes’ theorem, the risk that you will have a child is less than one in a billion. So there is no need to worry about the consequences."[66]

 

            Given SSA and the stated assumptions, it is easy to see that the snake’s argument is sound. We have  and using SSA, . We can assume that the prior probability of getting pregnant (based on ordinary empirical considerations) after sex is very roughly one half, . Thus, according to Bayes’ theorem, we have

 

 

Eve consequently has to conclude that the risk of her getting pregnant is negligible.

            This result seems quite counterintuitive. Most people’s intuition, at least at first glance, is that it would be irrational for Eve to think that the risk is that low. It seems foolish of her to act as if she were extremely unlikely to get pregnant – it seems contrary to empirical data. And we can assume she knows these data. We can assume that she has access to a huge pool of statistics, maybe based on some population of lobotomized human drones (lobotomized so that they don’t belong to the reference class, the class from which Eve should consider herself a random sample). Yet all this knowledge, combined with everything there is to know about the human reproductive system, would not change the fact that it would be irrational for Eve to believe that the risk of her getting pregnant is anything other than effectively nil. This is a strange result, but it follows from SSA.[67]

 

Experiment #2: Hunting with willpower

Our next example pushes the reasoning a little further and derives a consequence of an even greater degree of initial counterintuitiveness:

 

Assume as before that Adam and Eve were once the only people that existed, and that they know for certain that if they have a child they will be driven out of Eden and will proceed to have billions of offspring. But this time they have a foolproof way of generating a child (perhaps by advanced in vitro fertilization). Adam is tired of getting up every morning to go hunting. Together with Eve, he invents the following scheme: They form the firm intention that unless a wounded deer limps by their cave then they will have a child. They can then sit back and rationally expect with near certainty that a wounded dear – an easy target for Adam’s spear – will stroll by.

 

You can verify this result the same way as above, choosing appropriate values for the prior probabilities. The prior probability of a wounded deer limping by their cave that morning is one in ten thousand, say.

In the first experiment we had an example of what looked like anomalous precognition. Here we also have (more clearly than in the previous case) the appearance of psychokinesis. If the example works, which it does if we assume SSA, it almost seems as if Adam is causing a wounded deer to walk by. For how else could one explain the coincidence? Adam knows that he can repeat the procedure morning after morning and that he should expect a deer to appear each time. Some mornings he may not form the relevant intention and on those mornings no deer turns up. It seems too good to be mere coincidence; Adam is tempted to think he has magical causal powers.

 

Experiment #3: Eve’s card trick

One morning, Adam shuffles a deck of cards. At noon, Eve, having had no contact with the cards, decides to use her willpower to retroactively choose what card lies top. She decides that it shall have been the dame of spades. In order to ordain this outcome, Eve and Adam form the firm intention to have a child unless the dame of spades is top. They can then be virtually certain that when they look at the first card they will indeed find the dame of spades.

 

Here it looks as if the couple is in one and the same act performing both psychokinesis and backward causation – no mean feat before breakfast.

 

Experiment #4: The World Government

It is the year 2100 A.D. and certain technological advances have enabled the formation of an all-powerful and extremely stable world government, UN⁺⁺. Any decision about human action taken by the UN⁺⁺ will certainly be implemented. However, the world government does not have complete control over natural phenomena. In particular, there are signs that a series of n violent gamma ray bursts is about to take place at uncomfortably close distances in the near future, threatening to damage (but not completely destroy) human settlements. For each hypothetical gamma ray burst in this series, astronomical observations give a 90% chance that it will happen. In order to avert the crises, UN⁺⁺ makes the following plan: It will create a list of hypothetical gamma ray bursts, and for each entry on this list it decides that if the it the burst happens, it will build more space colonies so as to increase the total number of humans that will ever have lived by a factor of m. By arguments analogous to those in the earlier thought experiments, UN⁺⁺ can then be confident that the gamma ray burst will not happen, provided m is sufficiently great relative to n.

 

The main new feature of this experiment is that it depicts a situation that we can potentially actually bring about. Creating UN⁺⁺ might be practically difficult, and there is no guarantee that other preconditions are satisfied (that there are no extraterrestrials, for example); yet it is the sort of undertaking that could quite conceivably be accomplished though conventional non-magical means. This will be of relevance later when we discuss what SSA implies about our actual causal powers.

 

These four gedanken seem to show that SSA has some highly counterintuitive consequences: strange coincidences, precognition, psychokinesis and backward causation in situations where we would not expect such phenomena. If these consequences are genuine, they must surely count very heavily against the unrestricted version of SSA, with ramifications for DA and other applications forms of anthropic reasoning that rely on that principle.

However, we shall now see that such an interpretation misreads the experiments. A careful look at the situation reveals a different lesson: SSA, in interesting but rather subtle ways, avoids the worst of the purported implications.

Discussion of Experiment #2

In this section we will discuss Experiment 2. I think that the first and the third experiments can be analyzed along similar lines. Experiment 4 involves some additional complications which we will address in the next section.

Adam can repeat Experiment 2 many mornings.[68] And the experiment seems prima facie to show that, given SSA, there will be a series of remarkable coincidences between Adam’s procreational intentions and appearances of wounded deer. It was suggested that such a series of coincidences could be a ground for attributing paranormal causal powers to Adam.

The inference from a long series of coincidences to an underlying causal link can be disputed. Whether such an inference is legitimate would depend on how long is the series of coincidences, what are the circumstances, and also on what theory of causation one adopts. If the series were sufficiently long and the coincidences sufficiently remarkable, intuitive pressure would mount to give the phenomenon a causal interpretation; and one can fix the thought experiment so that these conditions are satisfied. For the sake of argument, we may assume the worst case for SSA, namely that if the series of coincidences occur then Adam will have anomalous causal powers. I will argue that even if we accept SSA, we should still think that neither strange coincidences nor anomalous causal powers would have existed if the experiment had been carried out.

We need to be careful when stating what is implied by the argument given in the thought experiment. All that was shown is that Adam would have reason to believe that his forming the intentions will have the desired outcome. The argument can be extended to show that Adam would have reason to believe that the procedure can be repeated; provided he keeps forming the right intentions, he should think that morning after morning, a wounded deer will turn up. If he doesn’t form the intention on some mornings, then on those mornings he should expect deer not to turn up. Adam thus has reason to think that wounded deer turn up on those and only on those mornings for which he formed the relevant intention. In other words, Adam has reason to believe there will be a coincidence. However, we cannot jump from this to the conclusion that there will actually be a coincidence. Adam could be mistaken. And he could be mistaken even though he is (as the argument in Experiment 2 showed, assuming SSA) perfectly rational.

Imagine for a moment that you are looking at the situation from an external point of view. That is, suppose (per impossible?) that you are an intelligent observer who is not a member of the reference class. Suppose you know the same non-indexical facts as Adam; that is, you know the same things as he does except such things as that "I am Adam" or "I am among the first two humans" etc. Then the probability you should assign to the proposition that a deer will limp by Adam’s cave one specific morning conditional on Adam having formed the relevant intention earlier that morning is the same as what we called Adam’s prior probability of deer walking by – one in ten thousand. As an external observer you would consequently not have reason to believe that there were to be a coincidence.[69]

Adam and the external observer, both being rational but having different information, make different predictions. At least one of them must be mistaken (although both are "right" in the sense of doing the best they can with the evidence available to them). In order to determine who was in fact mistaken, we should have to decide whether there would be a coincidence or not. Nothing said so far settles this question. There are possible worlds where a deer does turn up on precisely those mornings when Adam forms the intention, and there are other possible worlds with no such coincidence. The description of the thought experiment does not specify which of these two kinds of possible worlds we are referring to; it is underdetermined in this respect.

So far so good, but we want to be able to say something stronger. Let’s pretend there actually once existed these two first people, Eve and Adam, and that they had the reproductive capacities described in the experiment. We would want to say that if the experiment had actually been done (i.e. if Adam had formed the relevant intentions on certain mornings) then almost certainly he would have found no coincidence. Almost certainly, no wounded deer would have turned up. That much seems common sense. If SSA forced us to relinquish that conviction, it would count quite strongly as a reason for rejecting SSA.

            We therefore have to evaluate the counterfactual: If Adam had formed the relevant intentions, would there have been a coincidence? To answer this, we need a theory of conditionals. I will use a simplified version of David Lewis’ theory[70] but I think what I will say generalizes to other accounts of conditionals. Let w denote the actual world. (We are pretending that Adam and Eve actually existed and that they had the appropriate reproductive abilities etc.) To determine what would have happened had Adam formed the relevant intentions, we look at the closest[71] possible world w’ where he did do the experiment. Let t be the time when Adam would have formed the intentions. When comparing worlds for closeness to w, we are to disregard features of them that exclusively concern what happens after t. Thus we seek to find a world in which Adam forms the intentions and which is maximally similar to w in two respects: first, in its history up to t; and, second, in its laws. Is the closest world (w’) to w on these accounts and where Adam forms the intentions a world where deer turn up accordingly, or is it a world where there is no Adam-deer correlation?

            The answer is quite clearly that there is no Adam-deer correlation in w’. For such a w’ can be more similar to w on both accounts than can any world containing the correlation. Regarding the first account, whether there is a coincidence or not in a world presumably makes little difference as to how similar it can be to w with respect to its history up to t. But what difference it makes is in favor of no coincidence. This is so because in the absence of a correlation the positions and states of the deer in the neighborhood, at or shortly before t, could be exactly as in w (where none happened to stroll past Adam’s cave on the mornings when he did the experiment). The presence of a correlation, on the other hand, would entail a world that would be somewhat different regarding the initial states of the deer.

Perhaps more decisively, a world with no Adam-deer correlation would tend to win out on the second account as well. w doesn’t (as far as we know) contain any instances of anomalous causation. The laws of w do not support anomalous causation. The laws of any world containing an Adam-deer correlation, at least if the correlation were of the sort that would prompt us to ascribe it to an underlying causal connection, would contain laws supporting anomalous causation. By contrast, the laws of a world lacking the Adam-deer correlation could easily have laws exactly as in w. Similarity of laws would therefore also favor a w’ with no correlation.

Since there is no correlation in w’, the following statement is true: "If Adam had formed the intentions, he would have found no correlation". Although Adam would have reason to think that there would be a coincidence, he would find he was mistaken.

 

One might wonder: if we know all this, why can’t Adam reason in the same way? Couldn’t he too figure out that there will be no coincidence? – He couldn’t, and the reason is that he is lacking some knowledge you and I have. Adam has no knowledge of the future that will show that his creative hunting technique will fail. If he does his experiment and deer do turn up on precisely those mornings he forms the intention, then it could (especially if the experiment were successfully repeated many times) be the case that the effect should be ascribed to a genuine psychokinetic capacity. If he does the experiment and no deer turns up, then of course he has no such capacity. But he has no means of knowing that no deer turns up. The evidence available to him strongly favors the hypothesis that there will be a coincidence. So although Adam may understand the line of reasoning that we have been pursuing here, it will not lead him to the conclusion we arrived at, because he lacks a crucial premiss.

There is a puzzling point here that needs be addressed. Adam knows that if he forms the intentions then he will very likely witness a coincidence. But he also knows that if he doesn’t form the intentions then it will be the case that he will live in a world like w, where it is true that had he done the experiment he would most likely not have witnessed a coincidence. That looks paradoxical. Adam’s forming (or not forming) the conditional procreational intentions gives him relevant information. Yet, the only information he gets is about what choice he made. If that information makes a difference as to whether he should expect to see a coincidence, isn’t that just to say that his choice affects whether there will be a coincidence or not? If so, it would seem he has got paranormal powers after all.

A more careful analysis reveals that this conclusion doesn’t follow. The information Adam gets when he forms the intentions is about what choice he made. This information has a bearing on whether to expect a coincidence or not, but that doesn’t mean that the choice is a cause of the coincidence. It is simply an indication of a coincidence. Some things are good indicators of other things without causing them. Take the stock example: the barometer’s falling may be a good indicator of impending rain, if you knew something about how barometers work, but it is certainly not a cause of the rain. Similarly, there is no need to think of Adam’s decision to procreate if and only if no wounded deer limps by as a cause of that event, although it will lead Adam to rationally believe that that event will happen.

            One may feel that an air of mystery lingers on. Maybe we can put words to it as follows: Let E be the proposition that Adam forms the reproductive intention at time t = 1, let C stand for the proposition that there is a coincidence at time t = 2 (i.e. that a deer turns up). It would seem that the above discussion commits one to the view that at t = 0 Adam knows (probabilistically) the following:

 

(1)        If E then C.

(2)        If ¬E then ¬C.

(3)        If ¬E then "if E then it would have been the case that ¬C".

 

And there seems to be a conflict between (1) and (3).

I suggest that the appearance of a conflict is due to an equivocation in (3). To bring some light into this, we can paraphrase (1) and (2) as:

 

            (1’)      Prob_Adam (C|E)  1

            (2’)      Prob_Adam (¬C|¬E)  1

 

But we cannot paraphrase (3) as:

 

            (3’)      Prob_Adam (¬C|E)  1

 

When I said earlier, "If Adam had formed the intentions, he would have found no correlation", I was asserting this on the basis of background information that is available to us but not to Adam. Our set of background knowledge differs from Adam’s in respect to both non-indexical facts (we have observed the absence of any subsequent correlation between peoples’ intentions and the behavior of deer) and indexical facts (we know that we are not among the first two people). Therefore, if (3) is to have any support in the preceding discussion, it should be explicated as:

 

            (3’’)     Prob_We (¬C|E)  1

 

This is not in conflict with (1’). I also asserted that Adam could know this. This gives:

 

            (4)        Prob_Adam ("Prob_We (¬C|E)  1")  1

 

At first sight, it might seem as if there is a conflict between (4) and (1). However, appearances in this instance are deceptive.

Let’s first see why it could appear as if there is a conflict. It has to do with the relationship between Prob_Adam and Prob_We. We have assumed that Prob_Adam is a rational probability assignment (in the sense: not just logically consistent but "reasonable, plausible, intelligent" as well) relative to the set of background knowledge that Adam has at t = 0. And Prob_We is a rational probability assignment relative to the set of background knowledge that we have, say at t = 3. (And of course we pretend that we know that there actually was this fellow Adam at t = 0 and that he had the appropriate reproductive abilities etc.) But now, if we know everything Adam knew, and if in addition we have some extra knowledge, and if Adam knows that, then it is irrational of him to persist in believing what he believes. Instead he ought to adopt our beliefs, which he knows are based on more information. At least this follows if we assume, as we may in this context, that our a priori probability function is identical to Adam’s, and that we haven’t made any computational error, and that Adam knows all this. That would then imply (3’) after all, which would contradict (1’).

The fallacy in this argument is that it assumes that Adam knows that we know everything he knows. Adam doesn’t know that, because he doesn’t know that we exist. He may well know that if we exist then we will know everything (at least every objective – non-indexical – piece of information) that he knows and then some. But as far as he is concerned, we are just hypothetical beings.[72] So all that Adam knows is that there is some probability function, the one we denoted Prob_We, that gives a high conditional probability of ¬C given E. That gets him nowhere. There are infinitely many probability functions, and not knowing that we will actually exist he has no more reason to set his own credence equal to our probability function than to any other.

To summarize the results so far, what we have shown is the following: Granting SSA, we should think that if Adam and Eve had carried out the experiment, there would almost certainly not have been any strange coincidences. There is thus no reason to ascribe anomalous causal powers to Adam. Eve and Adam would rationally think otherwise but they would simply be mistaken. Although they can recognize the line of reasoning we have been pursuing they won’t be moved by its conclusion, because it hinges on a premiss that we – but not they – know is true. Good news for SSA.

One more point needs to be addressed in relation to Experiment 2. We have seen that what the thought experiments demonstrate is not strange coincidences or anomalous causation but simply that Adam and Eve would be misled. Now, there might be a temptation to see this by itself as a ground for rejecting SSA – if a principle misleads people it is not reliable and should not be adopted. However, this is a temptation to be resisted, because there is a good answer available to the proponent of SSA. Namely, as follows: It is in the nature of probabilistic reasoning that some people using it, if they are in unusual circumstances, will be misled. Eve and Adam were in highly unusual circumstances – they were the first two humans – so we shouldn’t bee too impressed by the fact that the reasoning based on SSA didn’t work for them. For a fair assessment of the reliability of SSA we have to look at how it performs not only in exceptional cases but in more normal cases as well.

            Compare the situation to the story about the Prison in chapter 4. There, remember, one hundred people were placed in one Prison and were asked to guess the color of the outside of their cell. Ninety cells were blue and ten were red. SSA recommended that a person in a cell thinks that with 90% probability she is in a blue cell. If all these people bet accordingly, 90% of them will win their bets. The unfortunate 10% who happen to be in red cells lose their bets, but it would be unfair to blame SSA for that. They were simply unlucky. Overall, SSA will lead 90% to win, compared to merely 50% if SSA is rejected and people bet at random. This consideration supports SSA.

            What about the "overall effect" of everybody adopting SSA in the three experiments we have been pondering above? Here the situation is more complicated because Adam and Eve have much more information than the people in the cells. Another complication is that we are considering a story where there are two competing hypotheses about the total number of people that will have existed. In both these respects the thought experiments are similar to DA and presumably no easier to settle. What we are trying to do in this chapter is examine some other features of SSA that are not salient in DA – namely that it seemed to lead to strange coincidences and anomalous causation.

Discussion of Experiment #4

Experiment 4 introduces a new difficulty. For although creating UN⁺⁺ and persuading it to adopt the plan would no doubt be a daunting task, it is the sort of project that we could quite conceivably carry out with non-magical means. Experiment 4 places us in more or less the same situation as Adam and Eve in the other three experiments. This twist demands that we carry the investigation one step further.

Let us suppose that if there is a long series of coincidences ("C") between items on the UN⁺⁺ list and failed gamma ray bursts then there is anomalous causation ("AC"). This supposition is more problematic than the corresponding assumption when we were discussing Adam and Eve. For the point of Experiment 4 is that it is claiming some degree of practical possibility, and it is not clear that this supposition could be satisfied in the real world. It depends on the details and on what view of causation one holds, but it could well be that the list of coincidences would have to be quite long before one would be inclined to regard it as a manifestation of an underlying causal link. And since the number of people that UN⁺⁺ would have to create in case of failure increases rapidly as the list grows longer, it is not clear that such a plan is feasible. But let’s set this scruple to one side in order to give the objection to SSA as good a shot as it can hope to have.

A first point is that even if we accept SSA, it doesn’t follow that we reason believe that C will happen. For we might think that it is unlikely both that UN⁺⁺ will ever be formed and that, if formed, it will adopt and carry out the relevant sort of plan. Without the UN⁺⁺ executing the plan, there is no reason to expect C (and consequently no reason to believe that there will be AC).

            But there is a more subtle way of attempting to turn Experiment 4 into an objection against SSA. One could argue that we know that we now have the causal powers to create UN⁺⁺ and make it adopt the plan; and we have good reason (given SSA) to think that if we do this then there will be C and hence AC. But if we now have the ability to bring about AC then we now, ipso facto, have AC. Since this is absurd we should reject SSA.

This reasoning is fallacious. Our forming UN⁺⁺ and making it adopt the plan would be an indication to us that there is a correlation between the list and gamma ray bursts. But it would not cause there to be a correlation unless we do in fact have AC. If we don’t have AC then forming UN⁺⁺ and making it adopt the plan (call this event "A") has no influence whatever on astronomical phenomena, although it misleads us to thinking we have. If we do have AC of the relevant sort, then of course the same actions would influence astronomical phenomena and cause a correlation. But the point is this: the fact that we have the ability to do A does not in any way determine whether we have AC. It doesn’t even imply that we have reason to think that we have AC.

            In order to be perfectly clear about this point, let me explicitly write down the inference I am rejecting. I’m claiming that from the following two premises:

 

(5) We have strong reasons to think that if we do A then we will have brought about C.

(6) We have strong reasons to think that we have the power to do A.

 

one cannot legitimately infer:

 

(7) We have strong reasons to think that we have the power to bring about C.

 

My reason for rejecting this inference is that one can consistently hold the conjunction of (5) and (6) together with the following:

 

(8) If we don’t do A then the counterfactual "Had we done A then C would have occurred" is false.

 

There might be a temptation to think that the counterfactual in (8) would have been true even if don’t do A. I suggest that this is due to the fact that (granting SSA) our conditional probability of C given that we do A is large. Let’s abbreviate this conditional probability ‘Pr(C|A)’. If Pr(C|A) is large, doesn’t that mean that C would (probably) have happened if we had done A? Not so. One must not confuse the conditional probability Pr(C|A) with the counterfactual "C would have happened if A had happened". For one thing, the reason why your conditional probability Pr(C|A) is large is that you have included indexical information (about your birth rank) in the background information. Yet one may well choose to exclude indexical information from the set of facts upon which counterfactuals are to supervene. (Especially so if one intends to use counterfactuals to define causality, which should presumably be an objective notion and therefore should not depend on indexical facts.)

So, to reiterate, even though Pr(C|A) is large (as stated in (5)) and even though we can do A (as stated in (6)), we still know that, given that we don’t do A, C almost certainly does not happen and would not have happened even if we had done A. As a matter of fact, we seem to have fairly good empirical grounds for thinking that we won’t do A. Experiment 4, therefore, does not show that we have reason to think that there is AC. – Again, good news for SSA.

 

Finally, although it may not be directly relevant to assessing whether SSA is true, it is interesting to ask: Would it be rational (given SSA) for UN⁺⁺ to adopt the plan?[73]

The UN⁺⁺ should decrease its credence of the proposition that a gamma ray burst will occur if it decides to adopt the plan. Its conditional credence Pr(Gamma ray burst | Plan adopted) is smaller than Pr(Gamma ray burst); this is what the thought experiment showed. Provided a gamma ray burst has a sufficiently great negative utility, non-causal decision theories would recommend that the plan be adopted.

What about causal decision theories? If a theory of causation is adopted according to which no AC would be involved even if C happens, then obviously causal decision theories would say that the plan is misguided and shouldn’t be adopted. The case is more complicated on a theory of causation that says that there is AC if C happens. UN⁺⁺ should then believe the following: If it adopts the plan, it will have caused the outcome of averting the gamma ray burst; if it doesn’t adopt the plan, then it is not the case that had it adopted the plan it would have averted the gamma ray burst. (This essentially just repeats (5) and (8).) The question is whether causal decision theories would in these circumstances recommend that UN⁺⁺ adopt the plan.

The decision that UN⁺⁺ makes gives it information about whether it has AC or not. Yet, it could be argued that when UN⁺⁺ deliberates on the decision, it can only take into account information available to it prior to the decision, and this information doesn’t suffice to determine whether it has AC. UN⁺⁺ therefore has to make its decision under uncertainty. Since on a causal decision theory UN⁺⁺ should do A only if it has AC, UN⁺⁺ would have to act on some preliminary guess about how likely it seems that AC; and since AC is strongly correlated with what decision UN⁺⁺ makes, it would also base its decision, implicitly at least, on a guess about what its decision will be. If it thinks it will eventually choose to do A, it has reason to think it has AC, and thus it should do A. If it thinks it will eventually choose not to do A, it has reason to think that it hasn’t got AC, and should thus not do A. UN⁺⁺ therefore seems to be faced with a somewhat degenerate decision problem in which it should choose whatever it preliminary guesses it will come to choose. More could no doubt be said about the decision theoretical aspects of this scenario, but I will leave it at that. Interested readers may compare the situation to the partly analogous case of the super-Newcomb problem presented in an appendix.

Conclusion

We have examined four gedanken designed to tease out some surprising consequences of SSA. In Experiment 2, it looked as though SSA implied strange coincidences and that Adam had psychokinetic powers. On closer analysis it turned out that it implies no such thing. It gives us no reason to think that there would have been coincidences or anomalous causation if Adam had carried out the experiment. SSA does lead Adam to think otherwise, but he would have been mistaken.

The fact that SSA would have misled Adam is no argument against it. For it is in the nature of probabilistic reasoning that in exceptional circumstances users will be mislead, and Adam is precisely such an untypically positioned observer. If we want to assess the reliability of reasoning based on SSA we have to look not only at the exceptional cases were it fails but also at the normal cases where it succeeds. In Prison (chapter 4), for example, SSA maximizes the fraction of all observers who are right.

Experiment 4 shifted the setting to one where we might actually have the potential to carry out the actions under investigation. We found that SSA does not give us reason to think that there will be strange coincidences or that we (or UN⁺⁺) have anomalous causal powers. However, there are certain (empirically implausible-looking) hypothetical circumstances under which it would. If we knew for certain that the UN⁺⁺ existed, and that it had the power to create humans in the requisite astronomical numbers and possessed the requisite stability to certainly carry out its original intentions, and that the other presuppositions behind the thought experiment were also satisfied – no extraterrestrials, all persons created are in the reference class, etc. – then SSA implies that we should expect to see the strange coincidences (intuitively: because this would make it enormously much less remarkable that we should have the birth ranks we have). But this is extremely unlikely.[74] Not all those who take the Doomsday argument in stride will roll over when faced with this implication.

All this notwithstanding, it is fair to describe the SSA-based recommendation to Eve, that she need not worry about getting pregnant, and the recommendation to Adam, that he should expect a wounded deer to walk by the cave given that he and Eve form the appropriate reproductive intentions, as remarkable and strongly counterintuitive. And yet, we seem forced to these conclusion if we accept the arguments for SSA given in chapter 4. The next chapter, which is the last chapter of the dissertation, suggests a way out of this dilemma.

Appendix: A SuperNewcomb problem

The following variant of the Newcomb problem may be compared to the answer to question 4 for the case where C would constitute a causal connection:

 

A SuperNewcomb problem. There are two boxes in front of you and you are asked to choose between taking only box B or taking both box A and B. Box A contains $1000. Box B will contain either nothing or $1,000,000. What B will contain is (or will be) determined by Predictor, who has an excellent track record of predicting your choices. There are two possibilities. Either Predictor has already made his move by predicting your choice and putting a million dollars in B iff he predicted that you will take only B (like in the ordinary Newcomb problem); or else Predictor has not yet made his move but will wait and observe what box you choose and then put a million dollars in B iff you take only B. In cases like this, Predictor makes his move before the subject roughly half of the time. However, there is a Metapredictor, who has an excellent track record of predicting Predictor’s choices as well as your own. You know all this. Metapredictor informs you of the following truth functional: Either you choose A and B, and Predictor will make his move after you make your choice; or else you choose only B, and Predictor has already made his choice. Now, what do you choose?

 

The added complication for causal decision theorists, compared to the ordinary Newcomb problem, is that you don’t know whether your choice will have a causal influence on the content of the box B. If Predictor made his move before you make your choice, then (let us assume) your choice doesn't affect what’s in the box. But if he makes his move after yours, by observing what choice you made, then you certainly do causally determine what B contains. In a sense the decision problem presented here is the opposite of the one faced by UN⁺⁺. There, a preliminary belief about what you will choose would be transformed into a reason for making that choice. Here, a preliminary decision would seem to undermine itself (given a causal decision theory). If you think you will choose two boxes then you have reason to think that your choice will causally influence what’s in the boxes, and so it seems you should take only one box. But if you think you will take only one box then you should think that your choice will not influence the contents, and thus you would appear to be led back to the decision to take both boxes; and so on.

CHAPTER 9: A THEORY OF OBSERVATIONAL SELECTION EFFECTS

In chapter 2 we established some preliminary conclusions regarding anthropic reasoning in cosmology. In chapter 3 we found what seemed to lie at the core of such reasoning and expressed it in the form of SSA. Chapter 4 presented arguments for applying SSA to a wide range of cases. Up to this point, it seemed that SSA could serve as the basis for a theory of observational selection effects and that all that remained was to fill in the details.

            Chapter 5 reviewed and analyzed the Doomsday argument. We identified what assumptions are needed in addition to accepting Model 2 for the God’s Coin Toss gedanken discussed in chapter 4 in order to derive the intended consequence. We also noted that there were a number of alternative conclusions that one could draw (other than that doom will strike soon) even were one persuaded that the basic structure of the argument is sound. That predictions such as those generated by DA should follow from a theory of observational selection effects may be surprising, but perhaps something we ought to feel ourselves driven towards – if there were no other problems this approach. Chapter 6 defended DA against a series of objections, and chapter 7 showed that SSA did not give rise to alleged paradoxical "observer-relative chances". All this pointed to the coherence and plausibility of basing a theory of observational selection effects on SSA, despite the fact that this would lead, in one small step, to DA.

            However, in chapter 8 we uncovered some rather shockingly counterintuitive consequences of an unrestricted use of SSA. Although a careful analysis revealed that these consequences do not include the prima facie implication that we should believe that we have paranormal causal powers, they do include advise to certain specially situated hypothetical agents (Adam and Eve, UN⁺⁺) to behave in ways which may appear to be quite foolish. These implications are not impossible to accept; John Leslie, for example, seems quite happy to bite the bullets. Yet many of us, endowed with less hardy epistemic teeth and stomachs, will find ingesting this meal of full metal jacket ammunition a deeply unsatisfying experience.

            In this chapter we therefore revisit the arguments for SSA given in chapter 4 and propose a modified version of SSA. This revised principle forms the basis of a new theory of observational selection effects, which I claim is the first one to meet the full range of success-criteria that we have established in the preceding investigations.

Criteria

Let’s list what some of these criteria are that any theory of observational selection effects should satisfy:

 

·        It must enable probabilistic observational consequences to be derived from typical cosmological theories. In particular, the theory should work for multiverse models and for big-single-universe models containing freak observers in a way that does not make a mockery of current scientific practice.

·        It should provide a framework for anthropic inference in other fields, including thermodynamics and evolutionary biology.

·        It must agree with intuitions in various thought experiments, including Prison, Emeralds, and Two Batches, and God’s Coin Toss. (A version of the God’s Coin Toss gedanken will be reassessed below.)

·        It should not yield the counterintuitive results we discovered in the four gedanken conducted in chapter 8. (If not strictly a success-criterion, this is at least a strong desideratum.)

·        Ideally, it should not support DA. (This is a weaker desideratum.)

·        But in achieving the two previous points, it must not rely on any of the objections against DA set out in the literature, since those are fallacious.

·        In particular, it should not incorporate SIA, or any supposition that amounts to the same thing.

·        It should account for everyday reasoning that involves observational selection effects, such as the example relating to traffic planning that we discussed in chapter 4.[75]

 

When these specific criteria and desiderata are combined with general theoretical goals – simplicity, coherence, non-arbitrariness, intuitive plausibility etc. – we have enough constraints that we should be very happy if we can find even one theory that fits them all. A theory that does that will, I believe, automatically be seen as attractive, maybe even compelling.

This chapter aims to propose such a theory.

The outlines of a solution

I suggest that in order to get the right approach to these complex problems, we first have to move from SSA to the more general SSSA. That gives us additional analytical firepower that will prove useful.

            Next, we home in on a key lesson that emerges from the preceding investigations: that the critical point, the fountainhead from which all the paradoxical results flow, seems to be the contexts where the hypotheses under consideration imply different numbers of observers. We find such contexts in the case of DA and the various Adam-and-Eve gedanken. By contrast, things seem to be working fine as long as the total number of observers is constant. This gives us an important clue. Recall that we found in chapter 4 that one type of cases where the definition of the reference class is relevant for what probability assignments we end up with are those where the total number of observers vary depending on which hypothesis is true. This suggests that the solution we’re looking for may have something to do with how the reference class is defined.

            To focus maximally on the core issue, therefore, let us think about the simplest possible case where the number of observers is a variable that we can use to model the reasoning that is at work in DA and the Adam-and Eve gedanken:

 

God’s Coin Toss, version three (G3). In an otherwise empty world, God tosses a fair coin. If it falls heads, He creates a room with one observer at time zero and creates an additional observer in the same room one hour later. If it falls tails, He creates a room with one observer at time zero but does not add any other observer. There is a clock on the wall, so everyone can see what time it is. Everyone knows the experimental setup. After two hours the experiment ends, and all observers are killed.

 

To avoid unnecessary complications, we can assume that there is one observer-moment in the first hour, and one or two observer-moments (depending on how the coin fell) in the second hour. We can depict the situation as follows:

 

 

This is similar to the original version of the God’s Coin Toss (G1) discussed in chapter 4, except that here the potential second observer begins to exist only after one hour and nobody is ignorant about their beard color.

In chapter 4, we considered three models for how to reason about G1. Rejecting Model 1 and Model 3, we were left with Model 2 – the model which we have subsequently seen leads to counterintuitive results. Is it perhaps possible that there is some other, better, way of reasoning that we have not yet considered and that could withstand the objections we found against Model 1 and Model 3? Let’s consider again, this time focusing on G3 (which provides a closer analogy to the problematic cases of Adam-and-Eve and DA) what are the probabilities that should be associated with each of the observer-moments.

            Now, if all these observer-moments would belong to the same reference class, then it follows from directly from SSSA that

 

P(Early | Tails) = 1/2, and

P(Early | Heads) = 1/3.

 

Together with knowledge that the coin toss was fair (P(Heads) = P(Tails) = 1/2)), Bayes’ theorem then implies:

 

P(Tails | Early) = 3/5

P(Heads | Early) = 2/5.

 

In words, we get a probability shift in favor of Tails, the hypothesis which would entail the smaller number of additional observer-moments.[76] This mirrors the finding that for example Adam’s reasoning gives him confidence that the event will happen (a wounded deer appearing) that would lead to there being fewer people in addition to Adam (the first person). It also mirrors DA, where we are urged to conclude that extinction events are more likely than previously thought, because they entail that there would be fewer additional people.

            This suggests that if we are unwilling to accept these consequences, then we should not place all observer-moments in G3 in the same reference class. Instead, we may segregate early observer-moments from late ones. A possible justification for doing this is that the early observer-moments are different from the later ones in ways that are not small or arbitrary but central to the problem at hand. The early observer-moments are ignorant about how the coin fell and are attempting to figure that out using some form of anthropic reasoning; the late observer-moments know the outcome of the coin toss and are not applying SSSA or anything like it.

If we do place early and late observer-moments in separate reference classes, then SSSA entails that early observer-moments should think there is a fifty-fifty probability of Heads. This is because the fraction of all observer-moments in their reference class who are observing what they (the early observer-moments) are observing is the same whether the coin fell heads or tails (namely, 1 in each case). SSSA here is interpreted as saying that each observer-moment should reason as if they were a random sample from all observer-moments in their reference class. This refinement of SSSA we can call SSSA-R (the "Strong Self-Sampling Assumption with a relativized reference class definition R"). We define it formally as follows.

Formalizing the theory: Equation SSSA-R

Let  be an observer-moment with a prior probability function . Let  be the class of all possible observer-moments that belong to the same reference class as  (according to R).[77] Let  be the possible world in which  is located. Let e be some evidence of the form "", where  is a class of possible observer-moments. Let h be some hypothesis, and let  be the class of possible observer-moments about whom h is true. (If h ascribes some property to a possible observer-moment then h is true about those and only those possible observer-moment that have the property in question; if h is non-indexical, not referring to any particular observer-moment, then h is true about all and only those possible observer-moments that live in possible worlds where h holds true.) Finally, let  be the class of observer-moments in the possible world w. We then have

 

                  (SSSA-R)

 

where  is a normalization constant given by

 

.

 

It may be helpful to illustrate the use of (SSSA-R) on the G3 gedanken described above.

 

 

The possible worlds w₁ and w₂ represent the following possibilities:

 

w₁: The coin fell heads.

w₂: The coin fell tails.

 

We can assume that the observer-moments share the prior P(w₁) = P(w₂) = 1/2. Let h be the hypothesis that the coin fell heads, and e the information available to an early observer-moment. If we use a reference class definition R that places early and late observer-moments in separate reference classes, we have

 

.

 

As can be seen in the diagram, we have

 

.

.

 

From this it follows that  and . That is, the early observer-moments are perfectly ignorant as to which way the coin fell.

Non-triviality of the reference class

We thus see how by focusing on observer-moments instead of observers as wholes, and by using non-universal reference classes, we avoid the counterintuitive consequences that flow from applying SSA with an unrestricted reference class in DA, the Adam-and-Eve and the UN⁺⁺ gedanken.

We justified placing some observer-moments in different reference classes in G3 by appealing to the differences between the observer-moments. For example, the difference between  and  was said to be "not small or arbitrary" but on the contrary "central to the problem at hand". A question that arises naturally at this stage is whether it is possible to say something more definite about the criteria for membership in an observer-moment’s reference class.

One beguilingly simple idea, which we shall however be forced to reject, is that the reference class for a given observer-moment consists of those and only those observer-moments from which it is subjectively indistinguishable:

 

           (R⁰)

 

Two observer-moments are subjectively indistinguishable iff they can’t tell which of them they are. (Being able to say "I am this observer-moment, not that one" does not count as being able to tell which observer-moment you are.) To give an example, if one observer-moment has a pain in the toe and another has a pain in the finger, they are not subjectively indistinguishable; for they can identify themselves as "this is the observer-moment with the pain in the toe" and "this is the observer-moment with the pain in the finger", respectively. By contrast, if two brains are in the precisely the same state, then – assuming epistemic states supervene on brain states – the two corresponding observer-moments will be subjectively indistinguishable. The same holds if the brains are in slightly different states but the differences are imperceptible to the subjects.

            If the two early observer-moments  and  are subjectively indistinguishable in G3, then we can directly apply this definition of the reference class (R⁰) and get the same result as above.

If  and  are subjectively distinguishable, we can still get the right answer with R⁰. In order to do that we need to modify the formal representation by considering a more fine-grained partition of the possibilities involved. Thus, to be concrete, suppose that the difference between  and  is that they have different pains (in toe vs. finger). Since early observer-moments do not know whether the finger-pain occurs in the two-person scenario (the coin falls heads) or in the one-person scenario (the coin falls tails), we have to consider four possible worlds in order to model the situation:

 

 

In this expanded representation, which is necessary if we want to use R⁰, we can explicitly model uncertainty as to whether it is the black-bearded observer or the red-bearded observer who has pain in his toe. The possible worlds w₁-w₄ represent the following possibilities:

 

w₁: The coin fell heads and the early observer has no pain in his finger.

w₂: The coin fell heads and the early observer has a pain in his finger.

w₃: The coin fell tails and the early observer has no pain in his finger.

w₄: The coin fell tails and the early observer has a pain in his finger.

 

We can assume that the observer-moments share the prior P(w_i) = 1/4 (for i = 1,2,3,4). Let h be the hypothesis that the coin fell heads, and e the information available to an early observer-moment with a toe-pain (i.e. without a finger-pain). By R⁰, the reference class for such an observer-moment is

 

.

 

As can be seen in the diagram, we have

 

.

 

From this it follows that  and . That is, in this version of God’s Coin Toss we get the same result with the minimalistic reference class definition R⁰ as we got on the revised approach of the previous section were we lumped all the early observer-moments together in the same reference class (and consequently a different result from the one on the original approach which used the maximally wide reference class definition where all observer-moments were in the same reference class).

So R⁰ can be made to work in this version of God’s Coin Toss even if the participants are never in subjectively indistinguishable states. This makes R⁰ look attractive – it’s a neat, clear-cut, non-arbitrary definition of the reference class, and applying SSSA-R with this reference class definition expunges all the counterintuitive implications stemming from using an unrestricted reference class as in the original approach. Unfortunately, there are cases where R⁰ does not work. In particular, recall the freak-observer-from-black-hole problem that we discussed in chapter 3 and 4. Suppose T1 and T2 are two theories that each postulate a big universe with black holes. According to T1, the vast majority of all observers observe values of physical constants in agreement with what we observe in the actual universe, and only a minority of freak observers are deluded and observe the physical constants having different values. According to T2 it is the other way around: the normal observers observe physical constants having other values than what we observe, and a small minority of freak observers make observations that agree with ours. Intuitively one would clearly want to say that our observations favor T1 over T2.[78] Yet this is not possible on R⁰. For according to R⁰, the reference class to which we belong consists of all and only those observers-moments who make these observations that we make – other observer-moments being subjectively distinguishable. If T1 and T2 both imply that the universe is big enough for it to be certain (or very probable) that it contains at least some observer making the observations that we are actually making, then on R⁰ our evidence would not favor T1 over T2. We can prove this formally as follows:

 

Consider an observer-moment , who, in light of evidence e, considers what probability to assign to the mutually exclusive hypotheses h_j (). By R⁰ we have .[79] SSSA-R⁰ then gives

.

Let  be the class of worlds where h_j is true and for which  is non-empty. We can thus write:

.

Since h_j is true in w_i if , we have , giving:

.

For each h_j which implies the existence of at least one observer-moment compatible with e[80],  is non-empty for each w_i in which h_j is true. For such a h_j we therefore have

 

.

 

Forming the ratio between two such hypotheses, h_j and h_k, we thus find that this is unchanged under conditionalization on e,

.

This means that e does not selectively favour any of the hypotheses h_j that implies that some observer-moment is compatible with e.

 

If this consequence is unacceptable, we have to reject R⁰ as a definition of the reference class. Any workable reference class definition must permit reference classes to contain observer-moments that are subjectively distinguishable; the reference class definition is in this sense non-trivial.

This shows that observer-moments that are incompatible with e have a role to play when working out the credence of observer-moments whose total evidence is e. It is worth emphasizing this important point further by means of a concrete example. Consider the following gedanken:

 

Blackbeards and Redbeards. Two theories, T1 and T2, are assigned equal prior probabilities. On T1 there three rooms: two of them contain observers with black beards and one contains an observer with red beard. On T2, there is one room with a black-bearded observer and two with red-bearded ones. Except for these rooms the world is empty, and the observers know what color their beard is (but they cannot see what’s in the other rooms). You find yourself in one of the rooms as a blackbeard. What credence should you give to T1?

 

Figure 9 depicts this setup.

 

 

By direct analogy to the cosmology case, we know that the answer should be that observing that you have a black beard gives you reason to favor T1 over T2. But if we use R⁰ as our definition of the reference class, we do not get that result.

In Figure 10, , , and  are the blackbeard observer-moments, and e is the information available to such an observer-moment ("This observer-moment is a blackbeard."). h is the hypothesis that T1 is true. Given SSSA-R⁰, then the observer-moments are divided into two reference classes: the blackbeards and the redbeards (assuming that they are not subjectively distinguishable in any other way than via their beard color). Thus, for example,  belongs to the reference class .

 

 

This gives  (). With R⁰, therefore, blackbeards’ credence of T1 is no greater than of T2.

A broader definition of the reference class will give the correct result. Suppose all observer-moments in Blackbeards and Redbeards are included in the same reference class:

 

 

This gives . That is, an observer-moment who observers black beard obtains some reason to think that T1 is true.

            This establishes boundaries for how the reference class can be defined. The reference class to which an observer-moment  belongs consists of those and only those observer-moments that are relevantly similar to . We have just seen that observer-moments can be relevantly similar even if they are subjectively distinguishable. And we saw before that if we reject the paradoxical recommendations in the Adam-and-Eve and UN⁺⁺ gedanken that follow from an unrestricted use of SSSA (or SSA), then we also know that not all observer-moments are relevantly similar. We thus have ways of testing suggestions for how to define the reference class. On the one hand they must not be so permissive as to give counterintuitive results in Adam-and-Eve and UN⁺⁺-type examples – Scylla. On the other hand, they must not be so stringent as to make cosmological theorizing impossible because of the freak-observer problem – Charybdis. Any approach that wishes to steer clear of paradox must avoid getting too close to either of these extremes.

            If C(R^U) is the universal class of possible observer-moments, and C(R⁰) is the class that only includes those observer-moments that are subjectively indistinguishable from , and if C() is the correct reference class for observer-moment , then we have in general:. Moreover, we have argued that there are cases in which we have (with strict inclusion):

 

                 (R-bounds)

 

Between these upper and lower bounds on the inclusively of the reference class there is room for diverging definitions which future investigations may explore, hopefully establishing further constraints or pinpointing a unique reference class as the correct choice.

SSA and SSSA as special cases of SSSA-R

We pointed out in chapter 4 that SSA is a special case of SSSA: SSA can be applied when all observers are similar in all relevant respects, whereas SSSA can be applied even when observers differ in regard to the amount of the relevant sort of subjective time they experience.

SSSA, in turn, can be seen as a special case of SSSA-R: SSSA can be applied when all possible observer-moments that would exist on some of the hypotheses under consideration are in the same reference class, whereas SSSA-R can be applied even to cases with more restrictive reference classes. SSSA thus follows from SSSA-R in those cases where have  for all observer-moments  that would exist on any of the hypothesis h_i under consideration (i.e. for which ). For with this reference class, we have  for all relevant worlds , which means that SSSA-R reduces to

 

                (SSSA-R^U)

.

 

SSSA, which says that each observer-moment  should reason as if they were a random sample from the class of all observer-moments, can be formalized using the framework developed in this chapter as

 

.

 

(This means that the prior probability of h is given by assigning all possible observer-moments a weight which is the inverse of the number of observer-moments in the world in which they live, multiplying this with the ordinary prior probability for that world, and then summing over all possible observer-moments for whom h is true.) Using P(h|e) = P(h&e) / P(e), it’s easy to see that this is identical to SSSA-R^U.

            A corollary of this is that any results regarding cases where all observers (observer-moments) are relevantly similar obtained using SSA (SSSA) remain valid on SSSA-R. This means that if we are persuaded by the intuitive correctness of some of those earlier results, we can use them to calibrate the reference class definition with which SSSA-R operates. One could therefore expect that SSSA-R will give at least as plausible results as SSA and SSSA when applied to those earlier examples. We will not go over again all the earlier examples but we shall look in some detail at the application to cosmology. This application is complex enough to illustrate most of the issues involved.

SSSA-R applied to cosmological fine-tuning

In chapter 2, we argued (among other things) for three preliminary conclusions regarding fine-tuning as evidence for multiverse hypotheses:

 

(1)   Fine-tuning favors (other things equal) hypotheses h₊ on which it is likely that one or more observer-containing universes exist over hypotheses h_- on which this is unlikely.

(2)   If two competing general hypotheses each imply that there is at least some observer-containing universe, but one of them implies a greater number of observer-containing universes, then fine-tuning is not a reason to favor the latter (other things equal).

(3)   Although P(e|h_M) may be much closer to zero than to one, it could nonetheless easily be large enough for e to favor the multiverse hypothesis.

 

We can now reexamine these theses in the new light from SSSA-R. To begin with (1), let’s determine under what circumstances we will have .

 

Suppose that

.

Since P(A|B) = P(A&B) / P(B), this can be expressed as

.

Similarly, if we suppose that

,

 

we get

.

If the hypotheses in question have about equal prior probability, , this implies that

                                        ($)

which is equivalent[81] to

         ($$)

Now, according to SSSA-R,  is equivalent to

          (£)

 

We may thus tell under what circumstances e will preferentially support h₊ over h_- by considering what is required for ($$) to yield (£). And from this we can learn three lessons:

 

·        If  for each  then (£) follows from ($$). This means that if all the observer-moments that the hypotheses say may exist and which are compatible with our evidence e are in the same reference class () then a hypothesis h₊ on which it is likely that one or more observer-moments compatible with e exist is supported vis-à-vis a hypothesis h_- on which that is unlikely.

·        In principle, it is possible for a hypothesis h_- which makes it less likely that there should be some observer-moment compatible with e to get preferential support from e vis-à-vis a hypothesis h₊ which makes that more likely. For example, if h₊ makes it likely that there should be one observer-moment compatible with e but at the same time makes it very likely that there are very many other observer-moments in our reference class which are not compatible with e, then h₊ may be disfavored by e compared to a hypothesis h_- on which it is quite unlikely that there should be any observer-moment compatible with e but on which also it is highly unlikely that there should be a substantial number of observer-moments in our reference class which are not compatible with e.

·        In practice (i.e. regarding (3)), if we think of h₊ as a multiverse theory and h_- as a single-universe theory, it seems that the concrete details will sometimes be such that (£) follows from ($$) together with the facts about these concrete details. This is the case when h₊ entails a higher probability than does h_- to there being some actual observer-moment that is compatible with e while at the same time the expected ratio between the number of actual observer-moments that are compatible with e that are in our reference class and the number of actual observer-moments that are in our reference class that are incompatible with e is about the same on h₊ as on h_- (or greater on h₊ than on h_-). Crudely put: it is ok to infer a bigger cosmos in order to make it probable that at least some observer-moment compatible with e exists, but only if this can be done without sacrificing too much of the desideratum of making it probable that a large fraction of the actual observer-moments that are in our reference class are compatible with e.

 

We’ll continue the discussion of (3) in a moment, but first let’s direct the spotlight on the second preliminary thesis. The analysis of (2) follows path parallel to that of (1).

 

Suppose that

Since the first expression implies that

we get, in a similar way as above,

          ($$*)

Meanwhile, by SSSA-R,  is equivalent to

         (£*)

 

Again we can compare ($$*) to (£*) to see under what circumstances the former implies the latter. We find that

 

·        Like before, if  for each  then (£*) follows from ($$*). This means that if the observer-moments that are compatible with e and with at least one of the hypotheses h₊₊ and h₊ are all in the same reference class () then a hypothesis h₊₊ on which it is likely that there are a great many observer-moments compatible with e is not preferentially supported vis-à-vis a hypothesis h₊ on which it is likely that there are relatively few observer-moments compatible with e.

·        Generally speaking, e will fail to distinguish between h₊₊ and h₊ if, for those observer-moments that are in our reference class, both hypotheses imply a similar expected ratio between the number of ones compatible with e and the number of ones incompatible with e. This means that ceteris paribus there is no reason to prefer a hypothesis which implies a greater number of observer-moments, beyond what is required to make it likely that there should be at least one actual observer-moment that is compatible with e.

 

Armed with these results, we can address (3). Let’s suppose for the moment that there are no freak observers.

First, consider a single-universe theory h_U on which our universe is fine-tuned, so that conditional on h_U there was only a very small probability that an observer-containing universe should exist. If we compare h_U with a multiverse theory h_M, on which it was quite likely that an observer-containing universe should exist, we find that if h_U and h_M had similar prior probabilities, then there are prima facie grounds for thinking h_M to be more probable than h_U given the evidence we have. Whether these prima facie grounds hold up on closer scrutiny depends on the distributions of observer-moments that h_U and h_M make probable. Supposing that the nature of the observer-moments that would tend to exist on h_U (if there were any observer-moments at all, which would improbable on h_U) are similar to the observer-moments that (most likely) exist on h_M, then we do in fact have such grounds.

The precise sense of the proviso that our evidence e may favor h_M over h_U only if the observer-moments most likely to exist on either hypothesis are of a similar nature is specified by SSSA-R and the lessons we derived from it above. But we can say at least something in intuitive terms about what sorts of single-universe and multiverse theories for which this will be the case. For example, we can consider the case where there is a single relevant physical parameter, . Suppose the prior probability distribution over possible values of  that a universe could have is smeared our over a broad interval (representing a priori ignorance about  and absence of any general grounds such as considerations of simplicity or theoretical elegance for expecting that  should have taken on a value within a more narrow range). In the archetypal case of fine-tuning, there is only a very small range of -values that give rise to a universe that contains observers. Then the conditional probability of e given h_U is very small. By contrast, the conditional probability of e given h_M can be quite large, since there will most likely be observers given h_M and these observer-moments will all be living in universes where  has a value within the small region of fine-tuned (observer-generating) values. In this situation, h_M would be preferentially supported by e.

            Now consider a different case which doesn’t involve fine-tuning but merely "ad hoc" setting of a free parameter. This is the case when observers can exist over the whole range of possible values of  (or a fairly large part thereof). The conditional probability of e given h_U is the same as before (i.e. very small), but in this case the conditional probability of e given h_M is about equally small. For although h_M makes it likely that there should be some observers, and even that there should be some observers compatible with e, h_M also makes it highly likely that there should be very many other observers that are not compatible with e. These are the observers that live in other universes in the multiverse, universes where  takes a different value than the one we have observed (and hence incompatible with e). If these other observers are in the same reference class as us (and there is no clear reason why they shouldn’t be, at least if the sort of observers living in universes with different  are not too dissimilar to ourselves), then this means that the conditional probability of e given h_M is very small. If enough other- universes contain substantial quantities of observers that are in the same reference class as us, then h_M will not get significant preferential support from e compared to h_U.

            We see here the sense in which fine-tuning suggests a multiverse in a way that mere free parameters do not. In the former case, h_M tends to be strongly supported by the evidence we have (given comparable priors), in the latter case not.

            On this story, how does one fit in the scenario where we discover a simple single-universe theory h_U^* that accounts for the evidence? Well, if h_U^* is elegant and simple, then we would assign it a relatively high prior probability. Since h_U^* by assumption implies or at least gives a rather high probability to e, the conditional probability of h_U^* given e would thus be high. This would be support for the single-universe hypothesis and against the multiverse hypothesis.

            One kind of candidate for such a single-universe theory are theories involving a creator who chose to create only one universe. If one assigned one such theory h_C^* a reasonably high prior probability, and if it could be shown to give a high probability to there being one universe precisely like the one we observe and no other universes, then one would have support for h_C^*. Creator-hypotheses on which the creator creates a whole ensemble of observer-containing universes would be less supported than h_C^*. However, if our universe is not of the sort that one might have suspected a creator to create if he created only one universe (if our universe is not the nicest possible one in any sense, for example), then the conditional probability of e on any creator-hypothesis involving the creation of only one universe might well so slim that even if one assigned such a creator-hypothesis a high prior probability it would still not be tenable in light of e if there were some plausible alternative theory giving a high conditional probability to e (e.g. a multiverse theory successfully riding on fine-tuning and its concomitant selection effects, or a still-to-be-discovered simple and elegant single-universe theory that fits the facts). If there were no such plausible alternative theory, then one may believe either a fine-tuned single-universe theory, a multiverse-theory not benefiting from observational selection effects, or a creator hypothesis (either of the single-universe or the multiverse kind) – these would be roughly on a par regarding how well they’d fit with the evidence (quite poorly for all of them) and the choice between them would be determined mainly by one’s prior probability function.

            In chapter 2 we also touched on the case where our universe is discovered to have some "special feature" F. One example of this is if we were to find inscriptions saying "God created this universe and it’s the only one he created." in places where it seems only a diving being would have made them (and we thought that there was a significant chance that the creator was being honest). Another example is if we find specific evidence that favors on ordinary (non-anthropic) grounds some physical theory that either implies a single-universe world or a multiverse. Such new evidence e’ would be conjoined with the evidence e we already have. What we should believe in the light of this depends on what conditional probability various hypotheses give to e&e’ and on the prior probabilities we give to these hypotheses. With e’ involving special features, e&e’ might well be such as to preferentially favor hypotheses that specifically accounts for the special features, and this favoring may be strong enough to dominate any of the considerations mentioned above. For example, if we find all those inscriptions, that would make the creator-hypothesis seem very attractive even if one assigned it a low prior probability and even if the conditional probability of there being a single universe with F given the creator-hypotheses would be small; for other plausible hypotheses would presumably give very much smaller conditional probabilities to our finding that our universe has F. (On h_U, it would be extremely unlikely that there would be any universe with F. On h_M, it might be likely that there should be some universe with F, but it would nonetheless be extremely unlikely that we should be in that universe, since on any plausible multiverse theory not involving a creator it would seem that if it were likely that there should be one universe with F then it would also be most likely that there are a great many other universes not having F and in which the observers, although many of them would be in the same reference class as us, would thus not be compatible with the evidence we have.) Similar considerations hold if F is not divine-looking inscriptions but something more of the nature of ordinary physical evidence for some particular physical theory.

            Finally, we have to tackle the question of how the existence of freak observers affects the story. The answer is: hardly at all. Although once we take account of freak observers there will presumably be a broad class of single-universe theories that make probable that some observers compatible with e should exist, this doesn’t help the case for such theories. For freak observers are random – whether they are generated by Hawking radiation or by thermal fluctuations or some other phenomena of a similar kind, these freak observers would not be preferentially generated to be compatible with e. Only an extremely minute fraction of all freak observers would be compatible with e. The case would therefore be essentially the same as if we have a multiverse where many universes contain observers (that are in our reference class) but only a tiny fraction of them contain observers that are compatible with e. Just as e didn’t especially favor such multiverse-theories over ad hoc single-universe theories, so likewise e is not given a sufficiently high probability by the there-is-a-single-universe-sufficiently-big-to-contain-all-kinds-of-freak observers theory (h_F) to make such a theory supported by our evidence. In fact, the case for h_F is much worse than the case for such a multiverse theory. For the multiverse theory, even if not getting any assistance from fine-tuning, would at least have a bias towards observers that have evolved (i.e. most observers would be of that kind). Evolved observers would tend to be in epistemic states that to some degree reflect the nature of the universe they are living in. Thus if not every logically possible universe is instantiated (with equal frequency) in the multiverse but instead the universes it contains tend to share at least some basic features with our actual universe, then a much greater fraction of the observers existing in the multiverse would be compatible with e than of the observers existing given h_F. On h_F the observers would be distributed roughly evenly over all logically possible epistemic states (of a given complexity)[82] whereas on the multiverse theory they’d be distributed over the smaller space of epistemic states that are likely to be instantiated in observers evolving in universes that share at least some basic features (maybe physical laws, or some physical laws, depending on the particular multiverse theory) with our universe. So h_F is strongly disfavored by e.

            Freak observers, therefore, cannot rescue an otherwise flawed theory. At the same time, the existence of freak observers would not prevent a theory which is otherwise supported by our evidence from still being supported once the freak observers are taken into account – provided that the freak observers make up a small fraction of all the observers that the theory says exist. In the universe we are actually living in, for example, it seems that there may well be vast numbers of freak observers (if only it is sufficiently big). Yet these freak observers would be in an astronomically small minority[83] compared to the regular observers that trace their origin to life that evolved by normal pathways on some planet. For every observer that pops out of a black hole, there are countless civilizations of regular observers. Freak observers can thus, on SSSA-R, be ignored for all practical purposes.

How the observation theory based on SSSA-R measures up against desiderata

The theory of reasoning under observational selection effects (an "observation theory" for short) that we have developed here builds on the ideas discovered in previous chapters. After establishing what an observation theory has to be able to do – the forms of reasoning that it must systematize and the sorts of considerations that it must be consistent with – and after analyzing how the simpler preliminary theory based on SSA works and the cases where it breaks down, we were led to propose the theory developed in the present chapter. This involved reassessing the earlier conclusions about the God’s Coin Toss gedanken by looking at it in a framework where observer-moments rather than observers are the basic entities. We argued that contrary to appearances, a model could be constructed in this framework that does not conflict with Bayesian kinematics, that rejects SIA, and that does not give rise to the sort of probability shift that leads to DA and the paradoxes discovered in chapter 8. This model involves placing certain observer-moments in different reference classes, and some arguments were given for why this was a legitimate procedure (although the main motivation is that it avoids the paradoxes of chapter 8). The ideas underlying this solution were generalized and given a mathematically precise expression in equation SSSA-R, which forms a centerpiece of the theory. Upper and lower bounds on the inclusively of the reference class were established (R-bounds), showing that the reference class is non-trivial.

            It was shown in some detail how this theory resolves the range of conundrums related cosmological theorizing and anthropic reasoning. The preliminary results derived in chapter 2 about the evidential relations between our evidence, single-universe and multiverse hypotheses, fine-tuning, and cosmic design hypotheses were confirmed, extended and made more precise using the new observation theory’s conceptual and formal resources. The theory permits probabilistic observational consequences to be derived in intuitive ways from both multiverse-models and big-single universe models and works fine even in the presence freak observers. Some reasons were given for why the theory will also work for the other applications of anthropic reasoning we have studied, although these cases were not explicitly analyzed in terms of SSSA-R.

            The observation theory undercuts DA by affording an alternative way of conceptualizing the God’s Coin Toss gedanken (G3), which is the common denominator of DA and the paradoxes of chapter 8. It provides a simple, uniform framework for drawing conclusions from data that have been subjected to observational selection effects. And it enables us to formulate specific further research objectives, including (but not limited to): explaining how to extend the theory to cover infinite cases; pinpoint and justify the correct definition of the reference class; applying it in detailed analyses in concrete scientific settings, especially multiverse cosmology and evolutionary biology; applying it to game theoretic problems involving imperfect recall; drawing out its philosophical implications for Lewis’ modal realism, the many-worlds and many-minds interpretations of quantum physics, physicist Max Tegmark’s speculative ideas for a theory of everything, hypotheses about intelligent extraterrestrial life and our own long-term future, and in general for theories about the large-scale structure of the world and the distribution of observers within it.

 

REFERENCES

Achinstein, P. (1993). "Explanation and 'Old Evidence'." Philosophia 51(1): 125-137.

Albert, D. D. (1989). "On the possibility that the present quantum state of the universe is the vacuum.". Proceedings of the 1988 biennial meeting of the philosophy of science association. A. Fine and J. Lepli. Michigan, East Lansing. 2: 127-133.

Angrilli, A., P. Cherubini, et al. (1997). Percept. Psychophys. 59: 972-982.

Aumann, R. J., S. Hart, et al. (1997). "The Forgetful Passenger." Games and Economic Behaviour 20: 117-120.

Barrow, J. D. (1983). "Anthropic definitions." Quarterly Journal of the Royal Astronomical Society. 24: 146-153.

Barrow, J. D. and F. J. Tipler (1986). The anthropic cosmological principle. Oxford; Oxford University Press.

Bartha, P. and C. Hitchcock (1999). "No One Knows the Date of the Hour: An Unorthodox Application of Rev. Bayes’s Theorem." Philosophy of Science (Proceedings) 66: S229-S353.

Bartholomew, D. J. (1984). The God of Chance. London, SCM Press Ltd.

Battigalli, P. (1997). "Dynamic Consistency and Imperfect Recall." Games and Economic Behaviour 20: 31-50.

Bigelow, J., J. Collins, et al. (1993). "The big bad bug: what are the Humean’s chances." British Journal for the Philosophy of Science 44: 443-63.

Black, R. (1998). "Chance, Credence, and the Principal Principle." British Journal for the Philosophy of Science 49: 371-85.

Bostrom, N. (1997). "Investigations into the Doomsday argument." Preprint http://www.anthropic-principles.com/preprints/inv/investigations.html.

Bostrom, N. (1998). "How Long Before Superintelligence?" International Journal of Futures Studies 2.

Bostrom, N. (1999). "The Doomsday Argument is Alive and Kicking." Mind 108(431):  539-50.

Bostrom, N. (1999). "A Subjectivist Theory of Objective Chance.". British Society for the Philosophy of Science Conference, July 8-9, Nottingham, U.K.

Bostrom, N. (2000). "Observer-relative chances in anthropic reasoning?" Erkenntnis 52: 93-108.

Bostrom, N. and et al. (1999). "The Transhumanist FAQ." http://www.transhumanist.org.

Brin, G. D. (1983). "The ‘Great Silence’: The Controversy Concerning Extraterrestrial Intelligent Life." Quarterly Journal of the Royal Astronomical Society 24: 283-309.

Buch, P. (1994). "Future prospects discussed." Nature 368(10 March): 108.

Carlson, E. and E. J. Olsson (1998). "Is our existence in need of further explanation?" Inquiry 41: 255-75.

Carter, B. (1974). "Large number coincidences and the anthropic principle in cosmology." Confrontation of cosmological theories with data. M. S. Longair. Dordrecht, Reidel: 291-8.

Carter, B. (1983). "The anthropic principle and its implications for biological evolution." Phil. Trans. R. Soc. A 310(347-363).

Carter, B. (1989). "The anthropic selection principle and the ultra-Darwinian synthesis.". The anthropic principle. F. Bertola and U. Curi. Cambridge, Cambridge university press: 33-63.

Castandeda, H.-N. (1968). "On the Logic of Attributions of Self-Knowledge to Others." Journal of Philosophy 65: 439-56.

Castaneda, H.-N. (1966). "’He’: A Study in the Logic of Self-Consciousness." Ratio 8: 130-57.

Castell, P. (1998). "A Consistent Restriction of the Principle of Indifference." British Journal for the Philosophy of Science 49: 387-395.

Caves, C. M. (2000). "Predicting future duration from present age: A critical assessment." Physics preprint archive astro-ph/0001414(24 Jan 2000).

Cirkovic, M. and N. Bostrom (2000). "Cosmological Constant and the Final Anthropic Hypothesis." Astrophys. Space Sci. in press.

Craig, W. L. (1988). "Barrow and Tipler on the anthropic principle vs. Divine design." British Journal for the Philosophy of Science 38: 389-395.

Craig, W. L. (1997). "Hartle-Hawking cosmology and atheism." Analysis 57(4): 291-295.

Delahaye, J.-P. (1996). "Reserchè de modeles pourl’argument de l’Apocalypse de Carter-Leslie". Unpublished manuscript.

Dieks, D. (1992). "Doomsday - Or: the Dangers of Statistics." Philosophical Quarterly 42(166): 78-84.

Dieks, D. (1999). The Doomsday Argument. Unpublished manuscript.

Dowe, P. (1998). Multiple universes, fine tuning and the inverse gambler’s fallacy.

Drexler, E. (1985). Engines of Creation: The Coming Era of Nanotechnology. London, Forth Estate.

Drexler, E. (1992). Nanosystems. New York, John Wiley & Sons, Inc.

Earman, J. (1987). "The SAP also rises: a critical examination of the anthropic principle." Philosophical Quarterly 24(4): 307-17.

Earman, J. (1992). Bayes or Bust? A Critical Examination of Bayesian Confirmation Theory. Cambridge, Massachusetts, The MIT Pres.

Eckhardt, W. (1992). "A Shooting-Room view of Doomsday." Journal of Philosophy 94(5): 244 - 259.

Eckhardt, W. (1993). "Probability Theory and the Doomsday Argument." Mind 102(407): 483-88.

Eells, E. (1990). "Bayesian Problems of Old Evidence.". Scientific Theories. Minneapolis, University of Minn. Pr.

Efstathiou, G. et al. (1995). "A model for the Infrared Continuum Spectrum of NGC-1068." Monthly Notices of the Royal Astronomical Society 277(3): 1134-44.

Elga, A. (2000). "Self-locating Belief and the Sleeping Beauty Problem." Unpublished Manuscript.

Feinberg, G. and R. Shapiro (1980). Life beyond Earth: The Intelligent Earthling’s Guide to Life in the Universe. New York, Morrow.

Feller, W. (1966). An Introduction to Probability Theory and its Applications. New York, Wiley.

Franceschi, P. (1998). "Une Solution pour l’Argument de l’Apocalypse." Canadian Journal of Philosophy 28(2): 227-246.

Franceschi, P. (1999). "Comment l’Urne de Carter et Leslie se Deverse dans celle de Hempel." Canadian Journal of Philosophy 29(1): 139-56.

Freitas(Jr.), R. A. (1999). Nanomedicine. Austin, Landes Bioscience.

Gale, G. (1981). "The Anthropic Principle." Scientific American 245 (June): 154-171.

Gale, G. (1996). "Anthropic-principle cosmology: physics or metaphysics?". Final Causality in Nature and Human Affairs. R. Hassing. Washington, D. C., Catholic University Press.

Gardner, M. (1986). "WAP, SAP, FAP &PAP." New York Review of Books 33(May 8): 22-25.

Gilboa, I. (1997). "A Comment on the Absent-Minded Driver Paradox." Games and Economic Behaviour 20: 25-30.

Gilovich, T., B. Vallone, et al. (1985). Cognitive Psychology 17: 295-314.

Goodman, S., N. (1994). "Future prospects discussed." Nature 368(10 March): 108.

Gott, R. J. (1993). "Implications of the Copernican principle for our future prospects." Nature 363(27 May): 315-319.

Gott, R. J. (1994). "Future prospects discussed." Nature 368(10 March): 108ff.

Gott, R. J. (1997). "A Grim Reckoning." New Scientist. 2108: 36-39.

Gould, S. J. (1985). The Flamingo’s Smile, Reflections in Natural History. London, Penguin Books.

Gould, S. J. (1990). "Mind and Supermind.". Physical cosmology and philosophy. New York, Collier Macmillan.

Greenberg, M. (1999). "Apocalypse Not Just Now." London Review of Books 1 July 1999: 19-22.

Grove, A. J. (1997). "On the Expected Value of Games with Absentmindedness." Games and Economic Behaviour 20: 51-65.

Hacking, I. (1987). "The inverse gambler’s fallacy: the argument from design. The anthropic principle applied to wheeler universes." Mind 76: 331-40.

Hall, N. (1994). "Correcting the guide to objective chance." Mind 103(412): 505-17.

Halpern, J. Y. (1997). "On Ambiguities in the Interpretation of Game Trees." Games and Economic Behaviour 20: 66-96.

Halpin, J. L. (1994). "Legitimizing Chance: The Best-System Approach to Probabilistic Laws in Physical Theory." Austl. J. Philosophy 72(3): 317-338.

Hanson, R. (1998). "Must early life be easy? The rhythm of major evolutionary transitions." Unpublished manuscript.

Hart, M. H. (1982). "Atmospheric Evolution, the Drake Equation, and DNA: Sparse life in an Infinite Universe.". Extraterrestrials: Where are they? M. H. Hart and B. Zuckerman. New York, Pergamon Press.

Hoefer, C. (1997). "On Lewis’ objective chance: ‘Humean supervenience debugged’." Mind 106(422): 321-34.

Hoefer, C. (1999). "A Skeptic’s Guide to Objective Chance". Unpublished manuscript.

Horwich, P. (1982). Probability and evidence. Cambridge, Cambridge University Press.

Howson, C. (1991). "The ‘Old Evidence’ Problem." British Journal for the Philosophy of Science 42(4): 547-555.

Kanitscheider, B. (1993). "Anthropic arguments - are they really explanations?". The Anthropic Principle: Proceedings of the Venice Conference on Cosmology and Philosophy. F. Bertola and U. Curi. Cambridge, Cambridge University Press.

Klapdor, H. V. and K. Grotz (1986). "Evidence for a nonvanishing energy density of the vacuum (or cosmological constant." Astrophysical Journal 301(L39-L43).

Kopf, T., P. Krtous, et al. (1994). "Too soon for doom gloom." Physics preprint gr-gc/9407002(v3, 4 Jul.).

Korb, K. and J. Oliver (1999). "A Refutation of the Doomsday Argument." Mind 107: 403-10.

Korb, K. B. and J. J. Oliver (1999). "Comment on Nick Bostrom’s "The Doomsday Argument is Alive and Kicking"." Mind 108(431): 551-3.

Kurzweil, R. (1999). The Age of Spiritual Machines: When computers exceed human intelligence. New York, Viking.

Kyburg(Jr.), H. (1981). "Principle Investigation." Journal of Philosophy 78: 772-777.

Larson, R. C. (1987). "Perspectives on Queues - Social-Justice and the Psychology of Queuing." Operations Research. 35(6): 895-904.

Leslie, J. (1972). "Ethically required existence." American Philosophical Quarterly July: 215-24.

Leslie, J. (1979). Value and Existence. Oxford, Blackwell.

Leslie, J. (1985). "Modern Cosmology and the Creation of Life.". Evolution and Creation. Notre Dame, Notre Came Press.

Leslie, J. (1985). "The Scientific Weight of Anthropic and Teleological Principles.". Conference on Teleology in Natural Science, Center for Philosophy of Science, Pittsburgh.

Leslie, J. (1988). "No inverse gambler’s fallacy in cosmology." Mind 97(386): 269-272.

Leslie, J. (1989). "Risking the world’s end." Bulletin of the Canadian Nuclear Society May, 10-15.

Leslie, J. (1989). Universes. London, Routledge.

Leslie, J. (1990). "Is the end of the world nigh?" Philosophical Quarterly 40(158): 65-72.

Leslie, J. (1992). "Doomsday Revisited." Philosophical Quarterly 42(166): 85-87.

Leslie, J. (1993). "Doom and Probabilities." Mind 102(407): 489-91.

Leslie, J. (1996). "The Anthropic Principle Today.". Final Causality in Nature and Human Affairs. R. Hassing. Washington, D. C., Catholic University Press.

Leslie, J. (1996). "A difficulty for Everett’s many-worlds theory." Int. Stud. Phil. Sci. 10(3): 239-246.

Leslie, J. (1996). The End of the World: the science and ethics of human extinction. London, Routledge.

Leslie, J. (1997). "Observer-relative Chances and the Doomsday argument." Inquiry 40: 427-36.

Lewis, D. (1986). Philosophical Papers. New York, Oxford University Press.

Lewis, D. (1994). "Humean Supervenience Debugged." Mind 103(412): 473-90.

Lipman, B. L. (1997). "More Absentmindedness." Games and Economic Behaviour 20: 97-101.

Mackay, A. L. (1994). "Future prospects discussed." Nature 368(10 March): 108.

Manson, N. A. (1989). Why Cosmic Fine-tuning Needs to be Explained. Department of Philosophy, Syracuse University.

Martel, H., P. R. Shapiro, et al. (1998). "Likely values of the cosmological constant." Astrophysical Journal 492(1): 29-40.

Martin, J. L. (1995). General Relativity. London, Prentice Hall.

Mayr, E. (1985). "The probability of extraterrestrial intelligent life.". Extraterrestrials, Science and alien intelligence. J. Edward Regis. New York, Cambridge University Press: 23-30.

McGrath, P. J. (1988). "The inverse gambler’s fallacy." Mind 97(386): 265-268.

McMullin, E. (1993). "Indifference Principle and Anthropic Principle in Cosmology." Stud. Hist. Phil. Sci. 24(3): 359-389.

Mellor, H. (1971). The matter of chance. Cambridge, Cambridge University Press.

Minsky, M. (1994). Will Robots Inherit the Earth? Scientific American. October.

Moravec, H. (1989). Mind Children. Harvard, Harvard University Press.

Moravec, H. (1998). "When will computer hardware match the human brain?" Journal of Transhumanism 1.

Moravec, H. (1999). Robot: mere machine to transcendent mind. New York, Oxford University Press.

Nielsen, H. B. (1981). "Did God have to fine tune the laws of nature to create light?". Particle Physics. L. Amdric, L. Dadic and N. Zovoko, North-Holland Publishing Company: 125-142.

Oliver, J. and K. Korb (1997). A Bayesian analysis of the Doomsday Argument, Department of Computer Science, Monash University.

Papagiannis, M. D. (1978). "Could we be the only advanced technological civilization in our galaxy?". Origin of Life. H. Noda. Tokyo, Center Acad. Publishing.

Papineau, D. (1995). "Probabilities and the many minds interpretation of quantum mechanics." Analysis 55(4): 239-246.

Papineau, D. (1997). "Uncertain decisions and the many-worlds interpretation of quantum mechanics." The Monist 80(1): 97-117.

Parfit, D. (1998). "Why anything? Why this?" London Review of Books Jan 22: 24-27.

Perlmutter, S., G. Aldering, et al. (1998). Nature 391(51).

Perry, J. (1977). "Frege on Demonstratives." Philosophical Review 86: 474-97.

Perry, J. (1979). "The Problem of the Essential indexical". Nous 13: 3-21.

Piccione, M. and A. Rubinstein (1997). "The Absent-Minded Driver’s Paradox: Synthesis and Responses." Games and Economic Behaviour 20: 121-130.

Piccione, M. and A. Rubinstein (1997). "On the Interpretation of Decision Problems with Imperfect Recall." Games and Economic Behaviour 20: 3-24.

Polkinghorne, J. C. (1986). One World: The Interaction of Science and Theology. London.

Ramsey, F. P. (1990). "Chance.". Philosophical Papers. D. H. Mellor. New York, Cambridge University Press.

Raup, D. M. (1985). "ETI without intelligence.". Extraterrestrials, Science and alien intelligence. J. Edward Regis. New York, Cambridge University Press: 31-42.

Redelmeier, D. A. and R. J. Tibshirani (1999). "Why cars in the other lane seem to go faster." Nature 401: 35.

Reiss, D. et al. (1998). "Constraints on cosmological models from Hubble Space Telescope observations of high-z supernovae." Astrophysical Journal 493(2).

Ross, H. (1992). Astronomical evidence for the God of the Bible. Unpublished manuscript.

Roush, S. (1998). "Doomsday, Pangloss and Doctor Who." Unpublished manuscript.

Sagan, C. (1995). "The abundance of life-bearing planets." Bioastronomy News 7(4): 1-4.

Schlesinger, G. (1991). The Sweep of Probability. Notre Dame, Indiana, University of Notre Dame Press.

Schopf(ed.), W. J. (1992). Major Events in the History of Life. Boston, Jones and Barlett.

Simpson, G. G. (1964). "The nonprevalence of humanoids." Science 143(769).

Singh, A. (1995). "Small nonvanishing cosmological constant from vacuum energy: Physically and observationally ." Physical Review D 52(12): 6700-7.

Sklar, L. (1989). "Ultimate explanations: comments on Tipler.". Proceedings of the 1988 biennial meeting of the philosophy of science association. A. Fine and J. Lepli. Michigan, East Lansing. 2: 49-55.

Sklar, L. (1993). Phyics and Chance: Philosophical issues in the foundations of statistical mechanics. Cambridge, Cambridge Univerity Press.

Skyrms, B. (1980). Causal necessity. London, Yale University Press.

Smith, Q. (1985). "The Anthropic Principle and Many-Worlds Cosmologies." Australasian Journal of Philosophy 63: 336-48.

Smith, Q. (1998). "Critical Notice: John Leslie, The end of the world." Candadian Journal of Philosophy 28(3): 413-434.

Smolin, L. (1997). The life of the cosmos. New York, Oxford University Press.

Snowden, R. J., N. Stimpson, et al. (1998). Nature 392: 450.

Strevens, M. (1995). "A closer look at the ‘new’ principle." ." British Journal for the Philosophy of Scienc. 46: 545-61.

Strevens, M. (1998). "Inferring Probabilities from Symmetries." Nous 32(2): 231-246.

Sturgeon, S. (1998). "Humean Chance: Five Questions for David Lewis." Erkenntnis 49: 321-335.

Swinburne, R. (1991). The Existence of God. Oxford, Oxford University Press.

Tännsjö, T. (1997). "Doom Soon?" Inquiry 40: 243-52.

Tegmark, M. (1996). "Does the universe in fact contain almost no information?" Foundations of Physics Letters 9(1): 25-42.

Tegmark, M. (1997). "Is "the theory of everything" merely the ultimate ensemble theory?" Physics preprints archive gr-gc/9704009(3 Apr).

Tegmark, M. (1997). "On the dimensionality of spacetime." Class. Quantum Grav. 14: L69-L75.

Thau, M. (1994). "Undermining and admissibility." Mind 103(412): 491-503.

Tipler, F. J. (1982). "Anthropic-principle arguments against steady-state cosmological theories." Observatory 102: 36-39.

Tipler, F. J. (1994). The Physics of Immortality: modern cosmology, God, and the resurrection of the dead. New York, Doubleday.

Tversky, A. and D. Kahneman (1981)." The Framing of Decisions and the Psychology of Choice." Science 211(4481): 453-8.

Tversky, A. and D. Kahneman (1991). "Loss aversion in riskless choice - a reference-dependent model." Quarterly Journal of Economics 106(4): 1039-1061.

van Inwagen, P. (1993). Metaphysics. Oxford, Oxford University Press.

Vranas, P. (1998). "Who’s Afraid of Undermining? Why the Principal Principle Need Not Contradict Humean Supervenience.". Sixteenth Biennial Meeting of the Philosophy of Science Association, Kansas City, Missouri.

Walton, D. and J. Bathurst (1998). "An exploration of the perceptions of the average driver’s speed compared to perceived driver safety and driving skill." Accident Analysis and Prevention 30(6): 821-830.

Weinberg, S. (1987). "Anthropic bound on the Cosmological Constant." Physical Review Letters 59(22): 2607-2610.

Wheeler, J. A. (1975). . The nature of scientific discovery. O. Gingerich. Washington, Smithsonian Press: 261-96 and 575-87.

Wheeler, J. A. (1977). Foundational problems in the special sciences. R. E. Butts and J. Hintikka. Dordrecht, Reidel: 3.

Whitaker, M. A. B. (1988). "On Hacking’s criticism of the Wheeler anthropic principle." Mind 97(386): 259-264.

White, R. (1999). Fine-tuning and multiple universes. Unpublished manuscript.

Wilson, P. A. (1991). "What is the explanandum of the anthropic principle?" American Philosophical Quarterly 28(2): 167-73.

Wilson, P. A. (1994). "Carter on Anthropic Principle Predictions." British Journal for the Philosophy of Science 45: 241-253.

Worrall, J. (1996). "Is the idea of a scientific explanation unduly anthropocentric? The lessons of the anthropic principle." Technical report. London, LSE: Centre for the philosophy of the natural and social sciences.

Zuboff, A. (1991). "One Self: The Logic of Experience." Inquiry 33: 39-68.