Self-Locating Belief in Big Worlds: Cosmology’s Missing Link to Observation*
[Preprint of the paper "Self-Locating Belief in Big Worlds: Cosmology's Missing Link to Observation." Journal of Philosophy. Vol. 99, No. 12 (2002).]
Space is big. It is very, very big. On the currently most favored cosmological theories, we are living in an infinite world, a world that contains an infinite number of planets, stars, galaxies, and black holes. This is an implication of most “multiverse theories”, according to which our universe is just one in a vast ensemble of physically real universes. But it is also a consequence of the standard Big Bang cosmology, if combined with the assumption that our universe is open or flat, as recent evidence suggests it is. An open or flat universe – assuming the simplest topology[1] – is spatially infinite at any time and contains infinitely many planets etc.[2]
Philosophical investigations relating to the vastness of the cosmos have focused on the fine-tuning of our universe. “Fine-tuning” refers to the alleged fact that the laws of physics are such that if any of several physical constants had been even slightly different, then life would not have existed. A philosophical cottage industry has arisen from the controversies surrounding issues such as whether fine-tuning is in some sense “improbable”, whether it should be regarded as surprising[3], whether it calls out for explanation (and if so whether a multiverse theory could explain it[4], whether it suggests ways in which current physics is incomplete[5], or whether it is evidence for the hypothesis that our universe was designed[6].
Here I wish instead to address a more fundamental problem: How can vast-world cosmologies have any observational consequences at all? I will show that these cosmologies imply, or give a very high probability to, the proposition that every possible observation is in fact made. This creates a challenge: if a theory is such that for any possible human observation that we specify, the theory says that that observation will be made, then how do we test the theory? What could possibly count as negative evidence? And if all theories that share this feature are equally good at predicting the data we will get, then how can empirical evidence distinguish between them?
I call this a “challenge” because current cosmological theories clearly do have connections to observation. Cosmologists are constantly modifying and refining theories in light of empirical findings, and they are presumably not irrational in doing so. But it is a philosophical problem to account for how this is possible.
One lesson that will emerge is that we must be careful about how we construe the evidence. We know not only that such-and-such observations are made (which we shall show is impotent as a basis for evaluating Big World theories): we also know that such-and-such observations are made by us. This indexical de se component of our evidence turns out to be crucial to cosmology, and recognizing this is the first step to the solution that I shall propose.
The second step is to formulate a new methodological principle that describes the probabilistic evidential bearing of (partly) indexical information on non-indexical hypotheses.
With the expanded evidence base and the new rule, we can explain how Big World theories are testable. We will also hint at how the epistemological theory we outline is useful in other areas of philosophy and scientific methodology.
But first, let us study in more detail how things go wrong if we construe the evidence non-indexically, in the form “Such-and-such an observation is made”. We can be generous and take “an observation” in a broad sense to include the total phenomenological content present in the observer’s mind. We do not, however, at this stage take “observing” as success verb, implying the veracity of observations; but rather, we assume an internal reading of the evidence. This assumption will later be relaxed.
I. THE CONUNDRUM
Consider a random phenomenon, for instance Hawking radiation. When black holes evaporate, they do so in a random manner such that for any given physical object there is a finite (although extremely small) probability that it will be emitted by any given black hole in a given time interval. Such things as boots, computers, or ecosystems have some finite probability of popping out from a black hole. The same holds true, of course, for human bodies and human brains in particular states.[7] Assuming that mental states supervene on brain states, there is thus a finite probability that a black hole will produce a brain in a state of making any given observation. Some of the observations made by such a brains will be illusory and some will be truthful. For example, some brains produced by black holes will have the illusory of experience of reading a measurement device that does not exist. Other brains, with the same experiences, will be making veridical observations – a measurement device may materialize together with the brain and may have caused the brain to make the observation. But the point that matters here is that any observation we could make has a finite probability of being produced by any given black hole.
The probability of anything macroscopic and organized appearing from a black hole is of course minuscule. The probability of a given conscious brain-state being created is tinier still. Yet even a low-probability outcome has a high probability of occurring if the random process is repeated often enough. And that is precisely what happens in our world, if the cosmos is very vast. In the limiting case where the cosmos contains an infinite number of black holes, the probability of any given observation being made is one.[8]
There are good grounds for believing that our universe is open and contains an infinite number of black holes. Therefore, we have reason to think that any possible human observation is in fact instantiated in the actual world.[9] Evidence for the existence of a multiverse would only add further support to this proposition.
It is not necessary to invoke black holes to make this point. Any random physical phenomenon would do. It seems we don’t even have to limit the argument to quantum fluctuations. Classical thermal fluctuations could, presumably, in principle lead to the molecules in a gas cloud containing the right elements to spontaneously bump into each other so as to form a biological structure such as a human brain.
The problem is that it seems impossible to get any empirical evidence that could distinguish between various Big World theories. For any observation we make, all such theories assign a probability of one to the hypothesis that that observation is made. That means that the fact that the observation is made is no reason whatever for preferring one of these theories to the others. Experimental results appear totally irrelevant.[10]
We can see this formally as follows. Let B be the proposition that we are in a Big World, defined as one that is big enough and random enough to make it highly probable that every possible human observation is made. Let T be some theory that is compatible with B, and let E be some proposition asserting that some specific observation is made. Let P be an epistemic probability function. Bayes’s theorem states that
P(T|E&B) = P(E|T&B)P(T|B) / P(E|B).
In order to determine whether E makes a difference to the probability of T (relative to the background assumption B), we need to compute the difference P(T|E&B) - P(T|B). By some simple algebra it is easy to see that
P(T|E&B) - P(T|B)
0 if and only if P(E|T&B)
P(E|B).
This means that E will fail to give empirical support to T (modulo B) if E is about equally probable given T&B as it is given B. We saw above that P(E|T&B)
P(E|B)
1. Consequently, whether E is true or false is irrelevant for whether we should believe in T, given we know B.
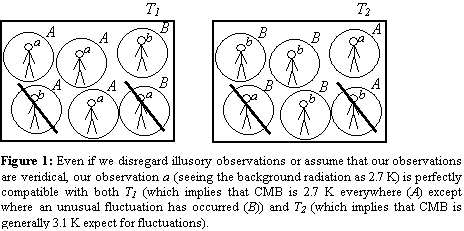
To illustrate, let T2 be some perverse permutation of an astrophysical theory T1 that we actually embrace. T2 differs from the T1 by assigning a different value to some physical constant. To be specific, let us suppose that T1 says that the temperature of the cosmic microwave background radiation is about 2.7 Kelvin (which is the observed value) whereas T2 says it is, say, 3.1 K. Suppose furthermore that both T1 and T2 imply that we are living in a Big World. One would have thought that our experimental evidence favors T1 over T2. Yet the above argument seems to show that this view is mistaken. Our observational evidence supports T2 just as much as T1. We really have no reason to think that the background radiation is 2.7 K rather than 3.1 K.
II. IT’S NOT THE OLD POINT ABOUT UNDERDETERMINATION OF THEORY BY DATA
At first blush, it could seem as if this simply rehashes the lesson, made familiar by Duhem and Quine, that it is always possible to rescue a theory from falsification by modifying some auxiliary assumption, so that strictly speaking no scientific theory ever implies any observational consequences. The above argument would then merely have provided an illustration of how this general result applies to cosmological theories. However, this would be to miss the point.
If the argument given above is correct, it establishes a much more radical conclusion. It purports to show that all Big World theories are not only logically compatible with any observational evidence, but they are also perfectly probabilistically compatible. They all give the same conditional probability (namely one) to every observation statement E defined as above. This entails that no such observation statement can have any bearing, whether logical or probabilistic, on whether the theory is true. If that were the case, it would not seem worthwhile to make astronomical observations if what we are interested in is determining which Big World theory to favor. The only reasons we could have for choosing between such theories would be either a priori (simplicity, elegance, etc.) or pragmatic (such as ease of calculation).
Nor is the argument making the ancient statement that human epistemic faculties are fallible, that we can never be certain that we are not dreaming or are brains in a vat. No, the point here is not that such illusions could occur, but rather that we have reason to believe that they do occur, not just some of them but all possible ones. In other words, we can be fairly confident that the observations we make, along with all possible observations we could make in the future, are being made by brains in vats and by humans that have spontaneously materialized from black holes or from thermal fluctuations. The argument would entail that this abundance of observations makes it impossible to derive distinguishing observational consequences from contemporary cosmological theories.
III. THE CONCLUSION IS A REDUCTIO
I trust that most readers will find this conclusion unacceptable. Cosmologists certainly appear to be doing experimental work and modify their theories in light of new empirical findings. The COBE satellite, the Hubble Space Telescope, and other devices are showering us with data that have been causing something of a renaissance in the world of astrophysics in recent years. Yet the argument described above would show that the empirical import of this information could never go beyond the humble role of providing support for the hypothesis that we are living in a Big World, for instance by showing that the universe is open. Nothing apart from this one fact could be learnt from such observations. Once we have established that the universe is open and infinite, then any further work in observational astronomy would be a waste of time and money.
Worse still, the leaky connection between theory and observation in cosmology spills over into other domains. Since nothing hinges on how we defined T in the derivation above, the argument can easily be extended to prove that observation does not have a bearing on any scientific question so long as we assume that we are living in a Big World.[11]
This consequence is absurd, so we should look for a way to mend the methodological pipeline and restore the flow of testable observational consequences from Big World theories. How can we do that?
IV. GIVING UP THE INTERNAL CONSTRUAL OF “OBSERVATION” DOESN’T SAVE US
Suppose we give up the internal construal of “observation” and instead take the term as a success verb, so that observing, say, a blue table implies that there is a blue table that is causally responsible for the observation. Suppose further that we couple this with the postulation that we are entitled (and perhaps even required) to have a prior credence function that strongly favors the hypothesis that we for the most part really do observe (in the success sense) what it seems to us that we are observing. Then it might appear as if we have an exit from our predicament. (Alternatively, we could formulate this escape plan by sticking to the original internal definition of “observation” and adding the postulate that our prior credence functions should strongly favor the veridicality of our observations.)
However, even setting aside foundationalist scruples, the proposed solution doesn’t get us out of the pickle.
To see this, consider that observers are not the only things that have a finite probability of being generated in random systems. On the same ground that we should expect human observers in all possible states to be ejected from black holes or to form from vastly improbable thermal fluctuations, we should also expect all physically possible local environments to spring forth. So not only are there observers having all sorts of illusions (of seeing a blue table or reading a measurement apparatus) but additionally there are observers making all sorts of veridical observations (actually seeing a blue table or reading off instruments in each of their possible output states). Consequently, even if we assume our observations to be veridical, we are still left with the problem that our current best theories give probability one to the existence of all possible such observations together with their truth-making local environments. (See Figure 1). We can even press on to the conclusion that for any possible human observation, there may be habitats in which that observation is appropriately caused by the observed object and in which the observer’s perceptions in general track her surroundings.[12]